Van der Waals equation: Units, Derivation, and Limitations

In 1873, J.D. Van der Waals modified the ideal gas equation for real gases by including the effect of Gas molecule interactions (attractive force between the molecules), as well as the molecules’ finite size (final volume of gas molecules). This equation is popularly known as Van der Waals equation.

The Van der Waals equation of state can be expressed as

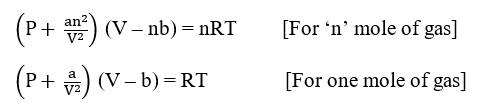
where ‘a’ and ‘b’ are known as van der Waals constant and are related to the intermolecular attractive forces between the gas molecules, and the volume of the molecules respectively.

Van der Waals equation derivation

Van der Waals modified the ideal gas equation by correcting two postulates of the kinetic molecular theory of gases and made it applicable for real gases. These two incorrect postulates according to Vander walls are:

• The gas molecules are so simple that their actual volume is negligible as compared to the total volume occupied by the gas.
• No effective force of attraction (intermolecular attraction) between molecules.

As a result, the ideal gas equation PV = nRT, derived on the basis of the kinetic molecular theory of gases could not be applied to real gases. In order for the ideal gas equation to be applicable to real gases, the pressure (P) and volume (V) elements in the ideal gas equation have to be corrected to make it applicable to real gases, according to van der Waal.

Corrected volume

According to the kinetic molecular theory of gases, volume of an ideal gas that corresponds to the volume of the container is negligible. But Vander Waals assumed that the real gases possess definite volume, and hence the volume of a real gas is considered as ideal volume minus the volume occupied by gas molecules.

Thus, the volume in the ideal gas equation is corrected as follows:

V – b, where b is the excluded volume

For n mole of gas, the corrected volume is (V – nb)

The excluded volume of the gas molecules is four times the actual volume of molecules.

Corrected Pressure

The pressure in real gas is created by the gas molecules colliding against the wall. However, the colliding molecules will be pulled inward by intermolecular attraction. As a result, the pressures exerted by molecules in real gases are lower than those in ideal gases.

P_real = P_ideal – p_a, where p is the pressure correcting term for real gases

P_ideal = P_real + p_a

The magnitude of the pressure correction term increases as the intermolecular interaction between gas molecules increases. Since, the molecules’ average pressure is reduced by Pa, which is proportional to the square of their density

p_a ∝ 1/V² [density = 1/V]

or, P_a = a/V² , where a is an der Waals constant

Thus, the pressure P in the ideal gas equation is corrected as:

Van der Waals equation

Now, substituting the corrected pressure and corrected volume in an ideal gas equation, PV = nRT, we get

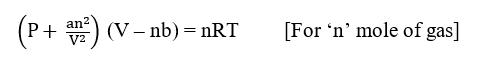
where, a & b are Van der Waals constants.

This equation is known as the van der Waals equation for n moles of a gas.

Unit of a and b in Van der Waals equation

• Unit of ‘a’ in van der Waals equation is atm litre² mol^–2
• Unit of ‘b’ in van der Waals equation is litre mol^–1 or m³ mol^–1

Limitations of Van der Waals equation

• Van der Waals equation fails at very high pressure and low temperature.

Van der waals equation Video

FAQ/MCQs

References

• J. D. Van der Waals, The equation of state for gases and liquids: Nobel Lecture, December 12, 1910″ (PDF). Nobel Lectures, Physics 1901–1921. Amsterdam: Elsevier Publishing Company. 1967. pp. 254–265
• Arun Bahl, B. S. Bahl & G. D. Tuli, Essentials of Physical Chemistry, S. Chand and Company Ltd., New Delhi, 2012.
• Silbey, Robert J.; Alberty, Robert A.; Bawendi, Moungi G. (2004). Physical Chemistry (4th ed.). Wiley