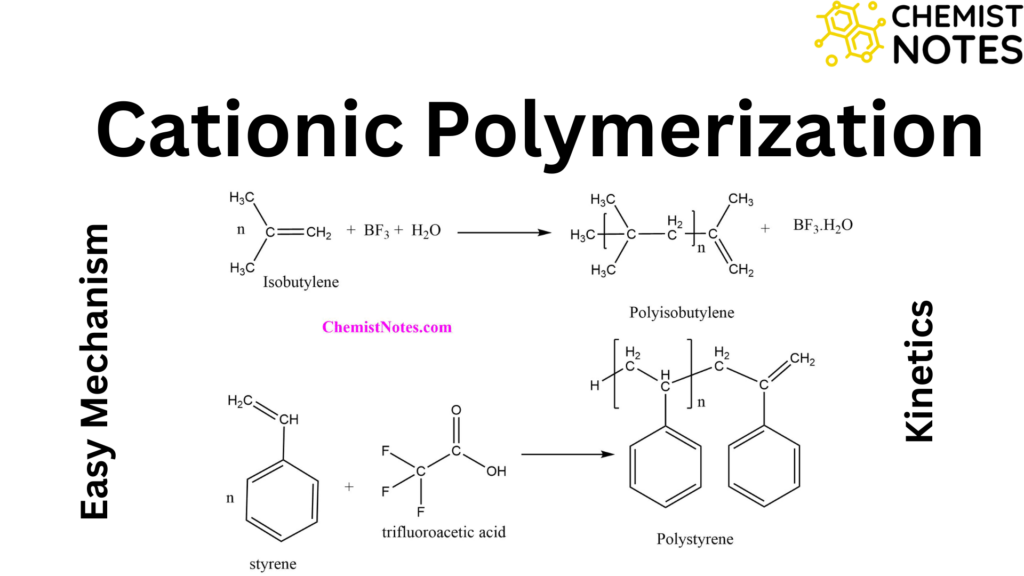
Table of Contents
ToggleIn 1860, James Clark Maxwell calculated the distribution of velocities over different fractions of molecules. This law of distribution is popularly called Maxwell distribution of molecular velocities.
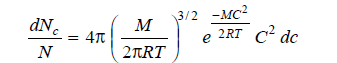
where dNc is the number of molecules having velocities between C and (C + dc), N is the total number of molecules, M is the molecular mass, and T is the absolute temperature (kelvin scale).
This relationship is called Maxwell’s law of distribution of velocities.
Every gas is made up of a large number of small particles known as molecules. Because these molecules are in a random state of constant rapid motion, they collide frequently with one another. When two molecules collide, one may transfer some of its kinetic energy to the other. The velocity of the molecule that gains energy rises while the velocity of others falls. Since millions of such collisions occur every second, the velocities of molecules are constantly changing.
Since the number of molecules is very large, a fraction of molecules will have the same particular velocity. As a result, there is a wide range of velocities across a varied fraction of molecules. Although it is impossible to determine the speeds of individual molecules, it is possible to calculate the distribution of velocities over different fractions of molecules using probability considerations. This distribution is called the Maxwell-Boltzmann distribution.
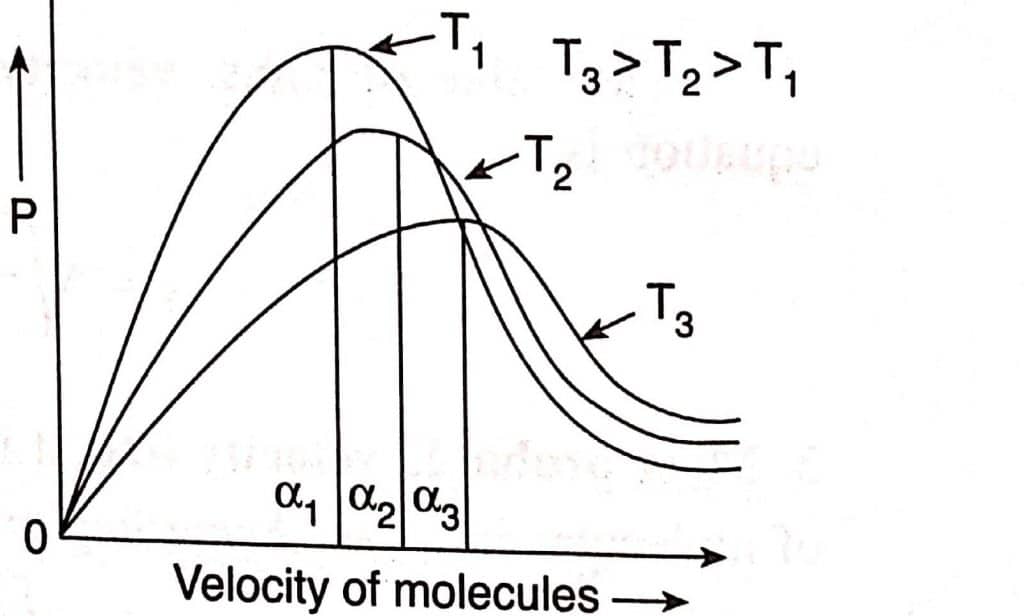
Maxwell plotted the fraction of molecules (p) with various velocities against their velocities at various temperatures. This curve is known as the Maxwell distribution curve.
Features of Maxwell distribution of velocities
- A very small fraction of molecules has either very low (close to zero) or very high velocities.
- The velocities of most intermediate fractions of molecules are close to the average velocity shown by the curve’s peak. This is known as the most probable velocity. It can be defined as the velocity of the largest fraction of molecules corresponding to the Maxwellian curve’s highest point.
- The entire curve shifts to the right at higher temperatures. This demonstrates that when the temperature rises, the number of molecules with greater velocity increases while the number of molecules with lower velocities decreases.
It’s important to note that the fraction of molecules with a particular velocity does not change as long as the gas’s temperature remains constant. The molecules with this velocity, however, may not be the same. This is due to the fact that during a collision, molecules with a specific velocity are changed, but their average number remains the same.
Molecular velocity
In the study of the kinetic molecular theory of gases, the following three types of velocities are considered:
Distribution of Molecular Velocities Video
References
- Raymond A. Serway; Jerry S. Faughn & Chris Vuille (2011). College Physics, Volume 1
- Arun Bahl, B. S. Bahl & G. D. Tuli, Essentials of Physical Chemistry, S. Chand and Company Ltd., New Delhi, 2012.