Table of Contents
ToggleLangmuir proposed an adsorption isotherm called Langmuir adsorption isotherm to theoretically explain type I adsorption. Freundlich adsorption isotherm that explains the empirical relation between the extent of adsorption (quantity of mass adsorbed by unit mass of solid adsorbent) and pressure is without any theoretical consideration but Langmuir tries to explain type I adsorption isotherm by making certain assumptions.
Assumptions of Langmuir Adsorption Isotherm
Some of the major Langmuir adsorption isotherm assumptions are:
- Adsorption is always monolayer.
- The adsorbed layer is homogeneous across the adsorbent.
- No interaction between the molecules that are adsorbed next to one another.
- Each adsorbent has different energy sites, but the adsorption energy (heat of adsorption) is the same for all of them.
- Adsorption is a reversible process. The rate of adsorption depends on the fraction uncovered and pressure.
Langmuir adsorption isotherm derivation
Langmuir proposed that gas molecules collide with a solid surface and get adsorbed. Some of these molecules then quickly evaporate or are ‘desorbed.’ Between the two opposing processes in an irreversible process, adsorption, and desorption, a dynamic equilibrium is eventually established.
Let be the fraction covered by a gas molecule, P the pressure, and () be the fraction uncovered by a gas molecule.
Since the rate of adsorption depends on the fraction uncovered and the pressure
i.e. rate of adsorption (1-θ)P
R1 = K1 (1-θ)P………………….(i)
Since the rate of desorption depends on the fraction covered
R2 = K2 θ……………………..(ii)
where K1 and K2 are adsorptions and desorption constant.
At equilibrium, the rate of desorption is equal to the rate of adsorption. So,
K1 (1-θ)P = K2 θ
K1P – K1θP = K2 θ
K1P = θ (K2 + K1P)

On rearranging the above Langmuir equation, a straight line equation should be obtained.
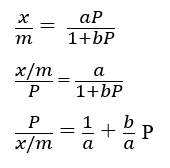
On plotting P/x against P, we should get a straight line with a slope equal to b/a and the intercept 1/a.
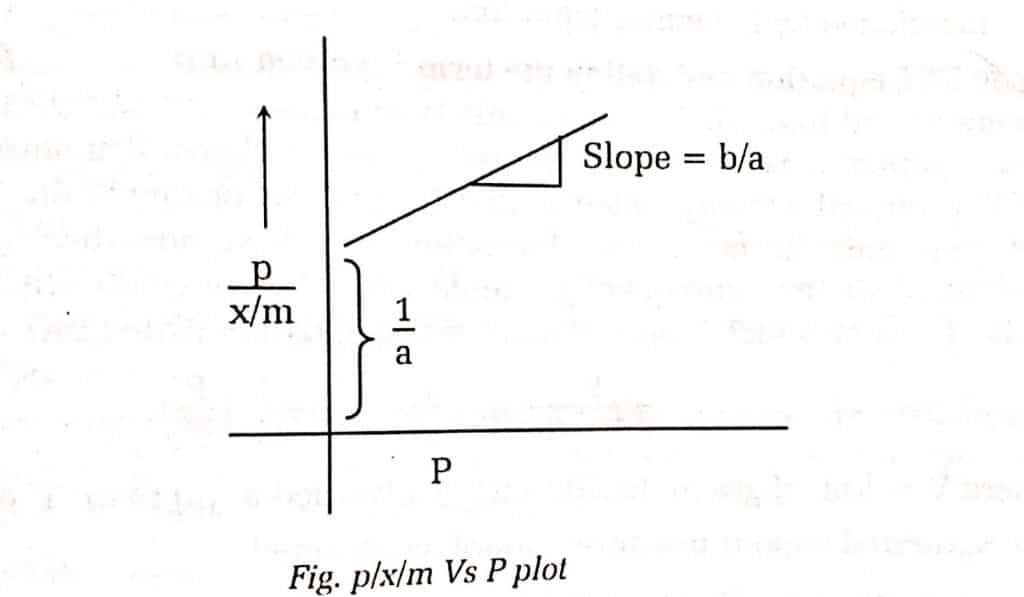
From the above graph, a straight line is obtained and hence verified Langmuir adsorption isotherm.
Limitations of Langmuir equation
- This equation works reasonably well at low pressure, but it cannot provide an exact relationship at high pressure i.e. Langmuir Isotherm is applicable at low pressures but fails at high pressures.

- Describe only the formation of the monolayer.
- The effect of temperature on adsorption is not considered.
- Relation between the heat of adsorption and surface area is not explained here.
Langmuir adsorption isotherm video
References
- Atkins, P. W.; De Paula, Julio; Keeler, James (2018). Atkins’ Physical chemistry (Eleventh ed.). Oxford, United Kingdom. ISBN 978-0-19-876986-6
- Arun Bahl, B. S. Bahl & G. D. Tuli, Essentials of Physical Chemistry, S. Chand and Company Ltd., New Delhi, 2012.
- Langmuir, Irving (1916). “Part I”. The Research Laboratory of the General Electric Company: 2221.
- Langmuir, Irving (1918). “Part II”. The Research Laboratory of the General Electric Company: 1848.