Table of Contents
ToggleSigmatropic rearrangement, a class of concerted pericyclic reactions, is controlled by orbital symmetry. During this rearrangement, a group connected by a sigma (σ) bond moves to the terminal of the neighboring pi (π)electron system. During the reaction, a σ bond appears to shift from one location to another and hence is called a sigmatropic rearrangement reaction. The π electrons also undergo a simultaneous shift. The number of π and σ bonds remain separately unchanged.
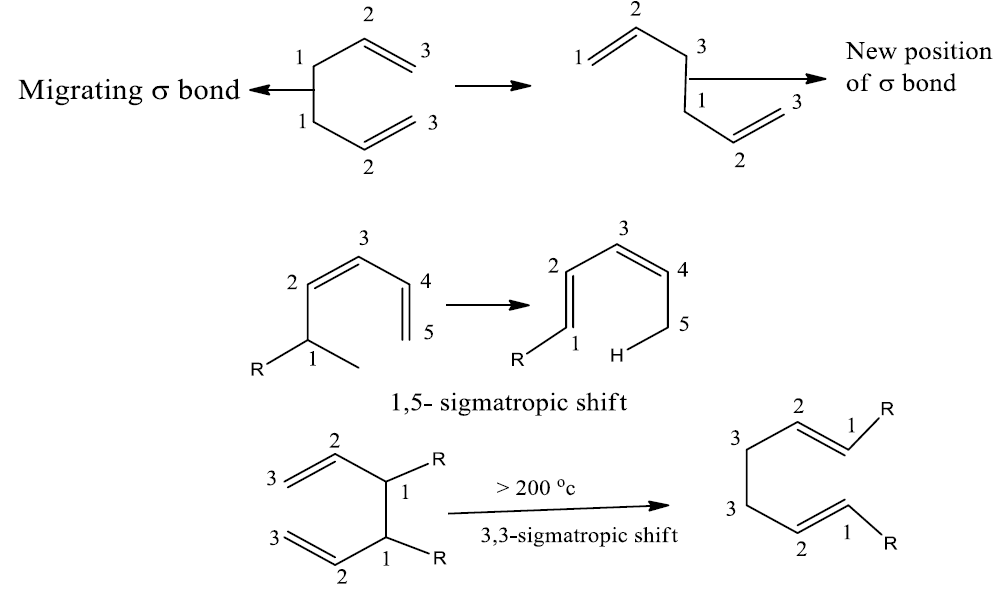
The relative position of the migrating atoms or groups is used to categorize sigmatropic rearrangements using a double-numbering method (i, j or m, n).
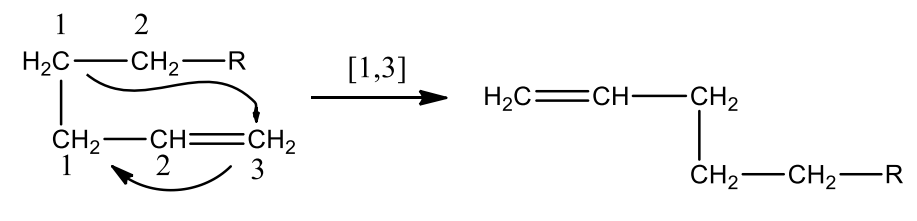
A sigmatropic reaction involves the migration of σ bond across a π system to another position within the system. Either one end or both ends of the bond can move and the π systems get rearranged as a result.

Sigmatropic Rearrangement
Sigmatropic rearrangement refers to the intramolecular movement of a group along a conjugated π system. A new σ bond is produced at the π system once the sigma bonds next to the conjugated π system are broken.
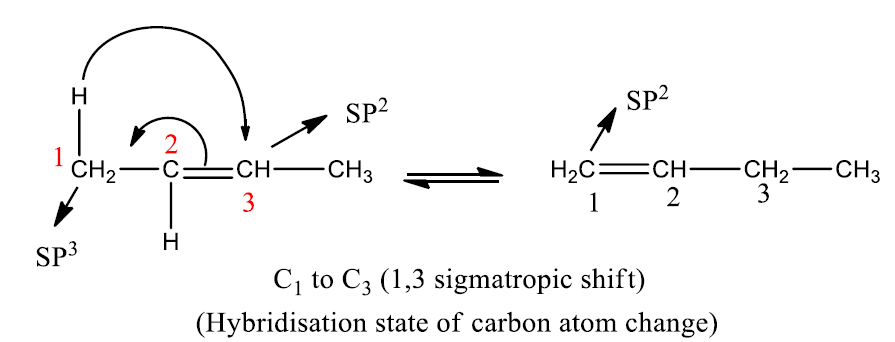
These reactions are classified according to a number of bonds separating the migration origin and migration terminus in each component. Migration of carbon takes place with the involvement of the p-orbital. p-orbital has two lobes of opposite phases.
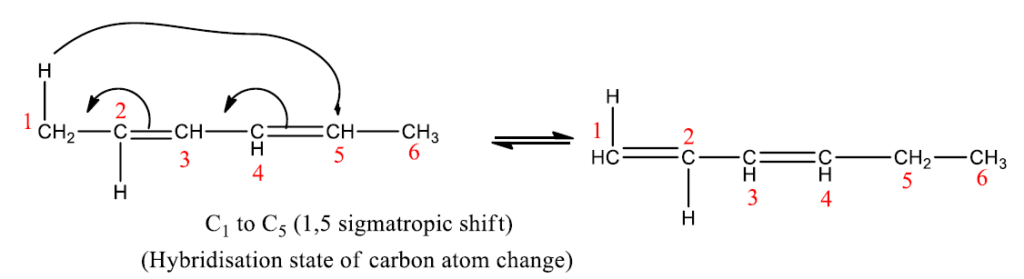
The number 3 and 5 indicates the migration terminus; the ‘1’ does not indicate the migration source, rather, it indicates that the bonding of the reactants and the products are to the same atom (no. 1) in the migrating group.
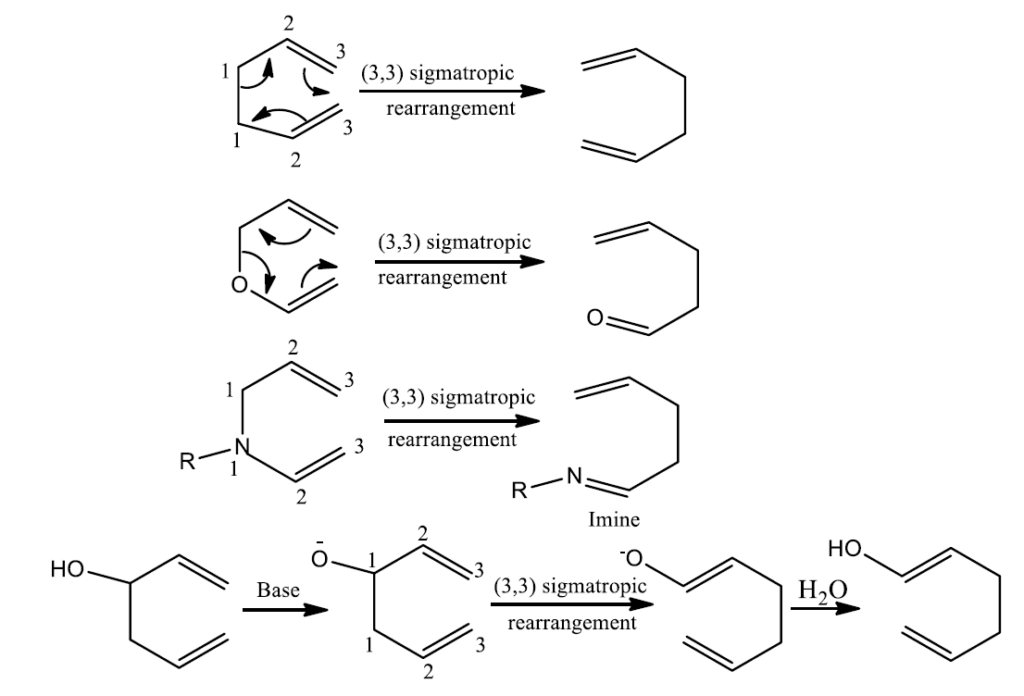
Some of the illustrations of rearrangement reactions are:
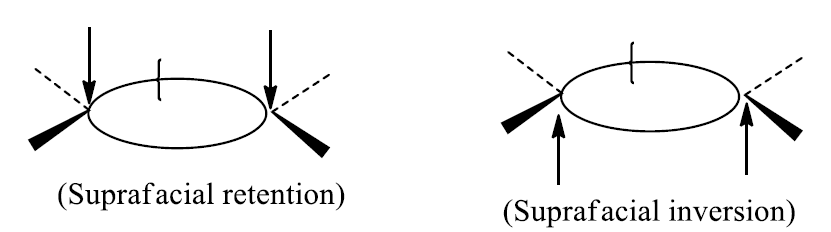
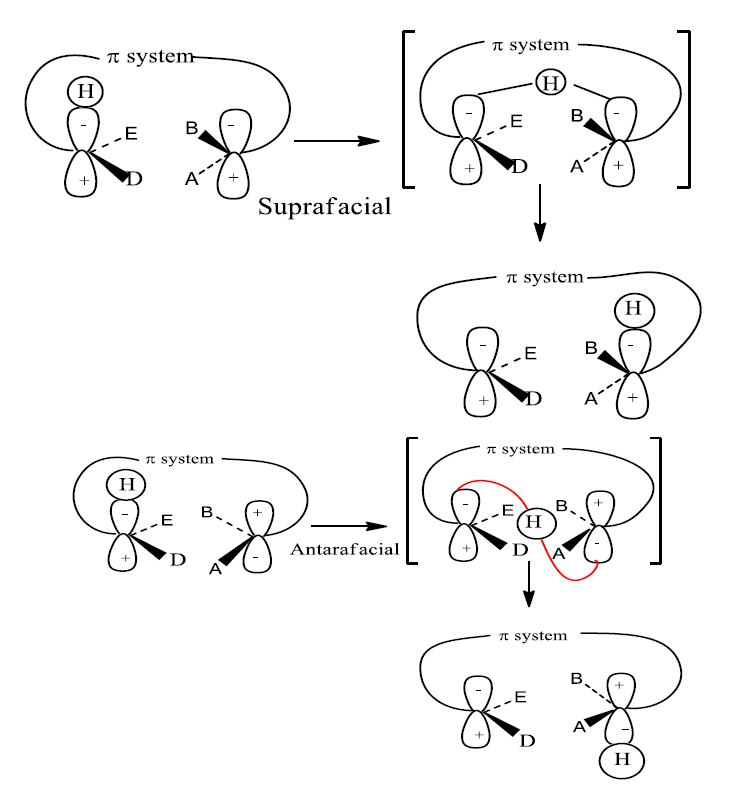
The new bond can theoretically be formed on either the same or opposite face of the π-framework. We distinguish between these processes by designating them suprafacial and antarafacial
- Addition of a σ bond is suprafacial if either retention or inversion occurs at both termini of reacting σ bond.
2. Addition of σ bond is antarafacial if retention occurs at one end and inversion occurs at the other end of the reacting σ bond.
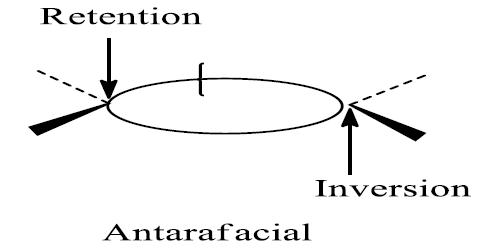
The other cycloaddition component is retained through the interaction with the head lobe of the σ bond. The other cycloaddition component interacts with the tail lobe of the σ bond during inversion.
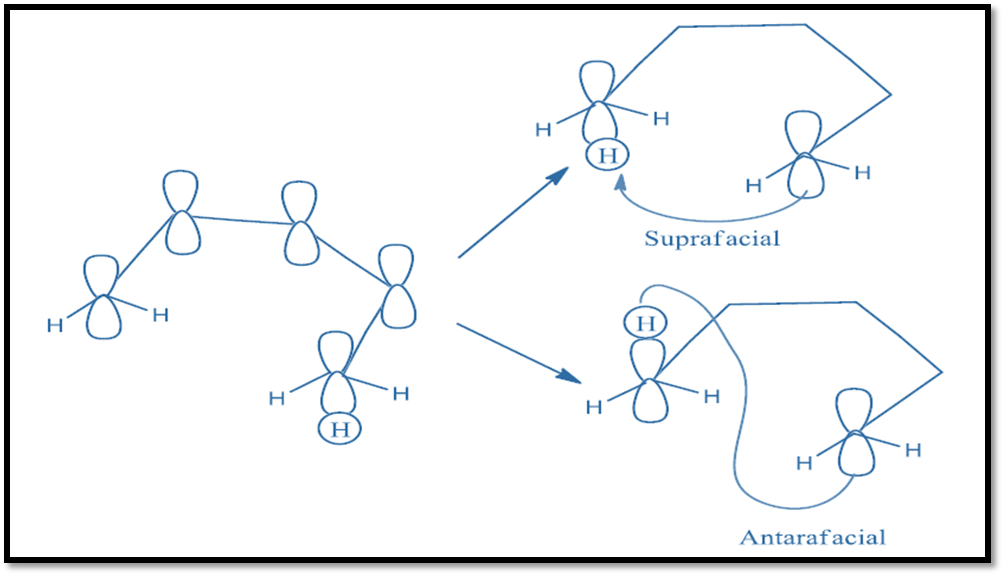
Moreover, the reaction takes place suprafacially and antarafacially as:
Clearly, suprafacial migration will usually be more feasible, geometrically also easily accessible than antarafacial migration. Nevertheless, when the length of the conjugated chain becomes large enough, it becomes possible for a bond to migrate from the up face to the bottom face of the conjugated system. Another point of interest is the inversion at the migrating center. The option of inversion is not available to a Hatom. The inversion can be experimentally observed or verified for asymmetric carbon. The ability of asymmetric to invert leads to the four possible migration routes. They are:
- Suprafacial with retention
- Suprafacial with inversion
- Antarafacial with retention
- Antarafacial with inversion
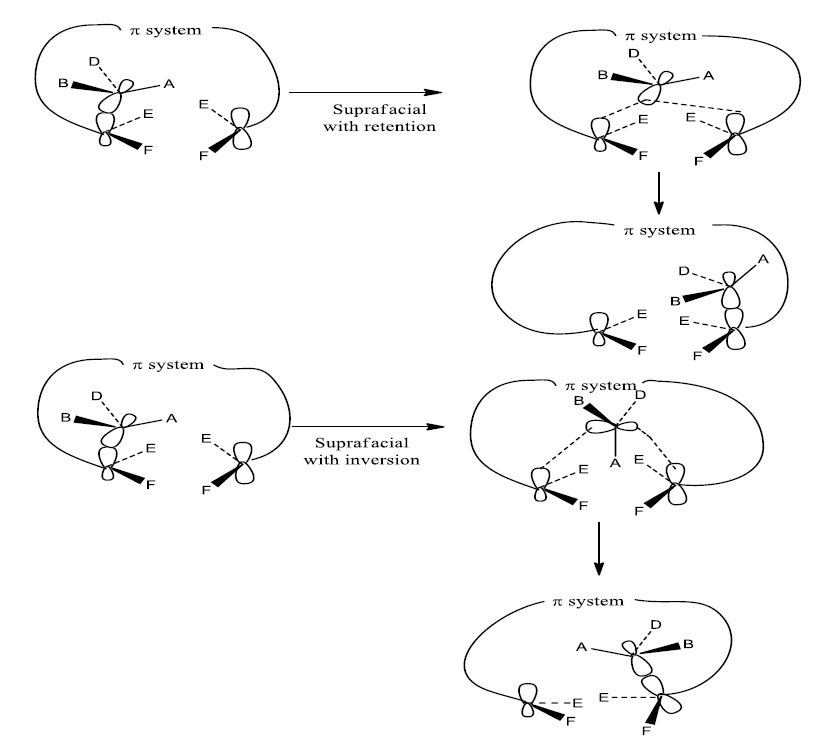
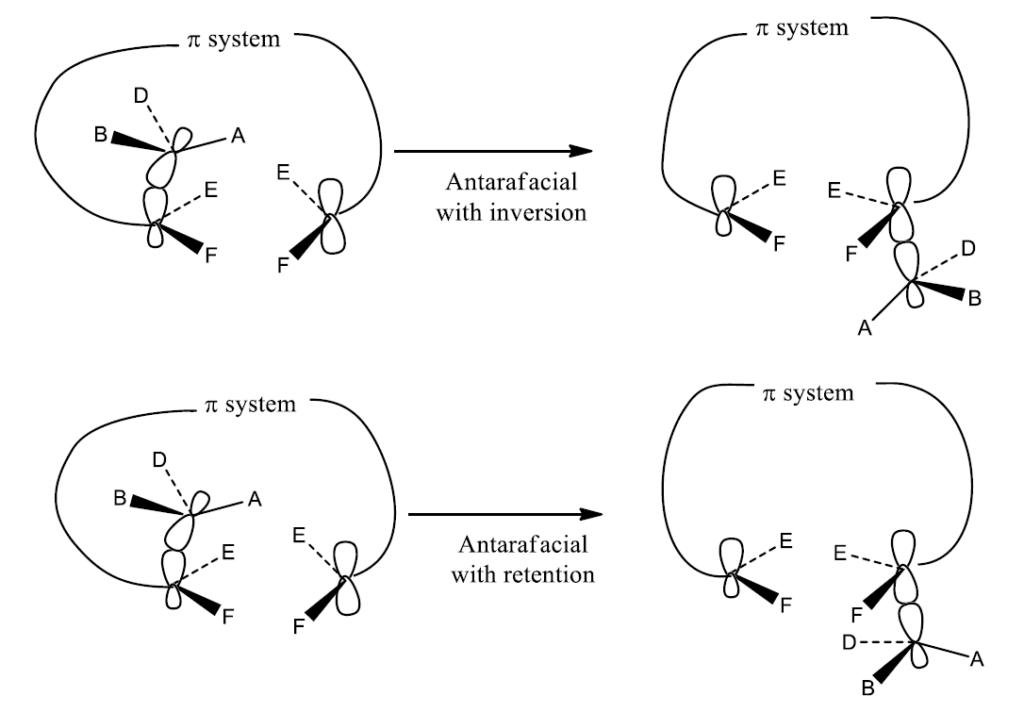
Mechanism of Sigmatropic Rearrangement Reaction
FMO Method
Let us consider the following reaction
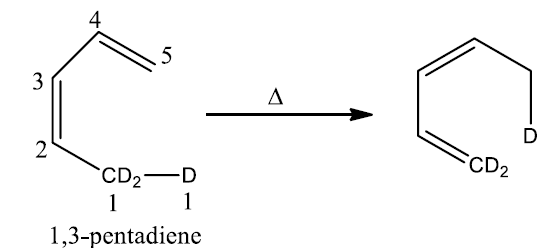
The sigmatropic transformation of 1,3-pentadiene to 1,5] takes place upon heating. The reaction can be easily depicted using the arrow. The arrow might go the either clockwise or anti-clockwise direction. This is not true for a polar reaction in which the convention is to run the arrow from pair of electrons towards the electron deficient.
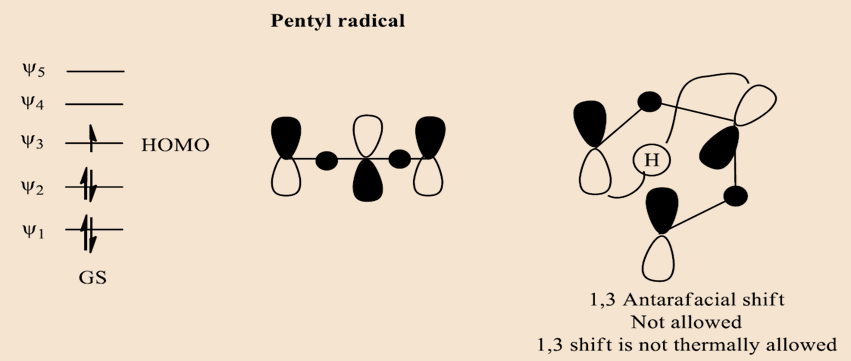
In the given example deuterium of sp3 hybrid carbon migrates onto the sp2 hybrid carbon (carbon-5). The given compound has also carbon-3 as sp2 hybrid carbon. Therefore, this compound can also give [1,3]-sigmatropic rearrangement on heating, but[1,3] shift is not observed.
Since thermal shifts are [1, 5], while photochemically induced shifts are [1, 3], any predicted mechanism must account for this difference. The frontier orbital method can be used to analyze such reactions and reveal their underlying mechanisms. Let’s start with the thermally induced sigmatropic rearrangement feasible, a [1, 3] shift.

The orbitals are analyzed under the assumption that the sigma bond connecting the moving group with its original site is homolytically cleaved to produce two free radicals. Since reaction occurs in a concerted manner, this is not how it happens. The analysis of molecular orbitals is, however, made possible by this assumption.

The products of the hypothetical cleavage are a hydrogen atom and an allyl free radical, which contains three p-orbitals. The π (pi) molecular orbitals of allyl free radical are shown as,
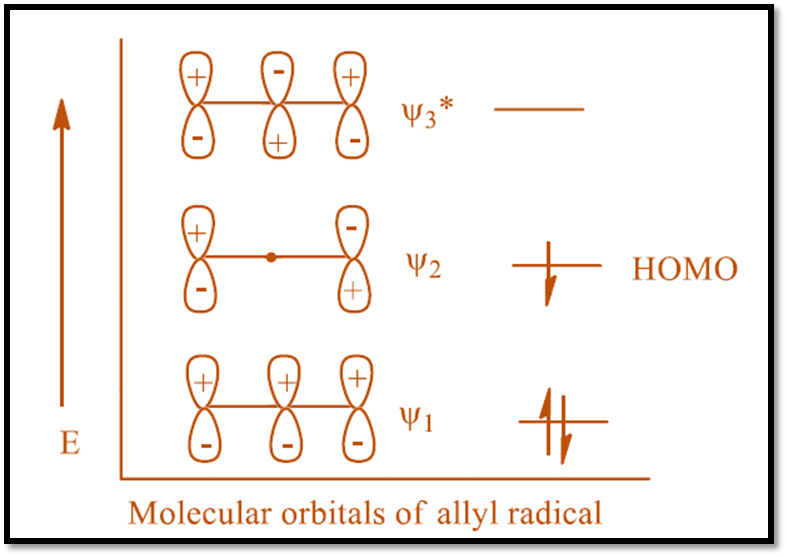
The actual hydrogen shift may occur either way. One possibility is that the migrating group stays on the same side of the (pi) orbital system. Such a migration is known as a suprafacial process. A suprafacial migration is geometrically possible but symmetry-forbidden in the thermal 1,3-sigmatropic rearrangement.
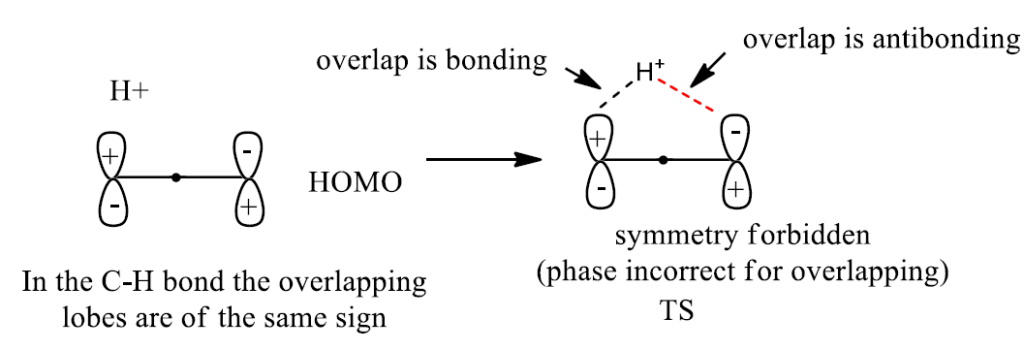
Let us consider the second mode of migration for a symmetry allowed [1, 3] sigmatropic shift to
occur, the migrating group must shift by an antarafacial process that is, it must migrate to the
the opposite face of the orbital system.
![[1, 3] sigmatropic shift](https://chemistnotes.com/wp-content/uploads/2023/04/S17.png)
[1,3]-sigmatropic shifts take place in the presence of UV light but examples are rare. Consider again what happens when a molecule absorbs a photon. LUMO of the ground state will become HOMO of the excited state known as photochemical HOMO.
![[1, 3] Sigmatropic shift](https://chemistnotes.com/wp-content/uploads/2023/04/image-24.png)
[1,5] Sigmatropic rearrangement
The products of hypothetical cleavage in this case are hydrogen free radicals and pentadienyl radicals. π MOs of pentadienyl radical are given below :
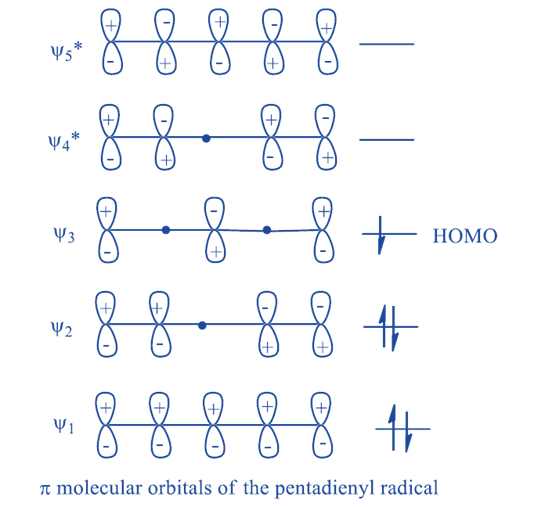
[1, 5] Sigmatropic shift is thermally allowed and photochemically forbidden. If we again assume a
homolytic bond cleavage for purpose of analysis, we must consider the molecular orbitals of
pentadienyl radical.
![[1, 5] Sigmatropic shift](https://chemistnotes.com/wp-content/uploads/2023/04/S20.png)
Consider photochemical [1, 5] sigmatropic rearrangement. In this case, ψ4* will be photochemical
HOMO.
![photochemical [1, 5] sigmatropic rearrangement](https://chemistnotes.com/wp-content/uploads/2023/04/S21.png)
Let us consider [1,5] sigmatropic shift takes place in thermal conditions:
![[1,5] sigmatropic shift](https://chemistnotes.com/wp-content/uploads/2023/04/s22.png)
In the case of the allyl radical,
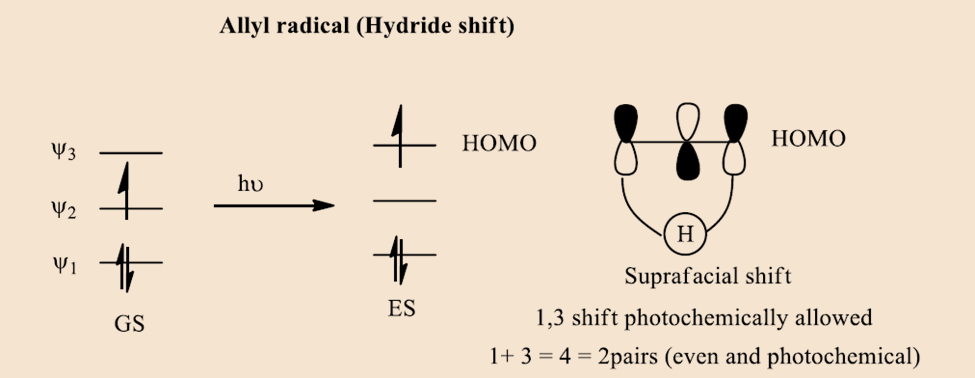
In case the case of pentyl radical,
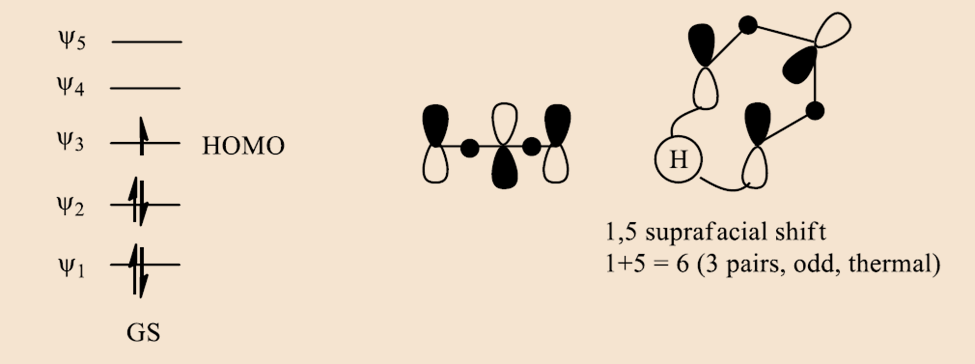
| Electrons | Thermal | Photochemical |
| 4n+2 | Suprafacial | Antarafacial |
| 4n | Antarafacial | Suprafacial |
The selection rules for sigmatropic hydrogen shift are:
| Electrons | Activation | Symmetry allowed |
| 4n (Even number of curved arrows) 1,3 (1+3) = 4 (2 pairs electrons) 1,7 (1+7) = 8 (4 pairs electrons) | Photochemical | Suprafacial |
| 4n+2 (Odd number of curved arrows) 1,5 (1+5) = 6 (3 pairs electrons) 1,9 (1+9) = 10 (5 pairs electrons) | Thermal | Suprafacial |
Stereochemical course for sigmatropic reactions
| i, j | Thermal reaction | Photochemical reaction |
| 1, 3 | Antarafacial | Suprafacial |
| 1, 5 | Suprafacial | Antarafacial |
| 1, 7 | Antarafacial | Suprafacial |
| 3, 3 | Suprafacial-Suprafacial or Antarafacial-Antarafacial | Suprafacial-Suprafacial |
Special points pertinent to sigmatropic changes are:
- Transformations taking place inside smaller to medium-sized rings are evidently unsuitable for antarafacial processes.
- It is feasible that a disrotatory carbon structure within the system will make it difficult or impossible to realize an asymmetrically allowed process, such as an antarafacial process, but this does not hold true for every scenario.
- Sigmatropic transitions among ionic species are accessible to orbital symmetry explanations. The [1,2] shift within the carbonium ion is therefore a symmetrically allowed shift.
Woodward-Hoffmann Selection Rule for Sigmatropic Reactions
| i + j | Ground State | Excited state |
| 4n | Antarafacial-suprafacial Suprafacial-Antarafacial | Suprafacial-Suprafacial Antarafacial-Antarafacial |
| 4n+2 | Suprafacial-Suprafacial Antarafacial-Antarafacial | Antarafacial-suprafacial Suprafacial-Antarafacial |
Sigmatropic Rearrangement Reactions Video
References
- R. B. Woodward and R. Hoffmann, Conservation of Orbital symmetry, Verlag Chemie GmbH, Academic Press, 1971.
- Charles DePuy and Orville L. Chapman, Molecular Reaction and Photochemistry, Prentice-Hall, 1972.
- Peter Skyes, A Guide book to mechanism in organic chemistry, sixth edition.