Table of Contents
ToggleCrystal field stabilization energy is the gain in energy achieved by the preferential filling up of orbitals by electrons. In other words, the reduction of a transition metal ion’s energy in a certain ligand environment is called crystal field stabilization energy (CFSE). The CFSE depends on factors like geometry, spin pairing energy, the number of d electrons, and ligand character (spectrochemical series), among others.
Crystal Field Stabilization Energy
Crystal field stabilization energy is defined as the change in energy due to the splitting of the d-orbitals of metal cation under the influence of ligand field in a complex. The stability of the complex increases as the amount of CFSE increases. Consequently, it is the magnitude of the energy difference between the two sets (t2g and eg ) orbitals.
Crystal field stabilization energy formula
The formula for CFSE in an octahedral complex with a dp+q configuration with p electrons in t2g and q electrons in eg orbitals is given by:
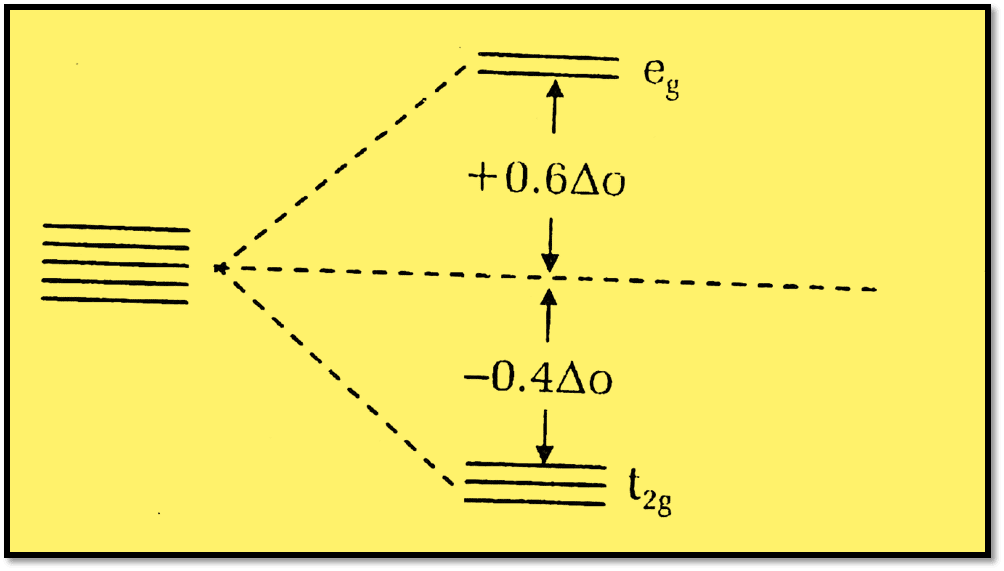
CFSE = (-0.4p + 0.6q)Δo + mP
or, CFSE = (-4p + 6q)Dq + mP
Where m = number of paired electrons, and P = mean pairing energy
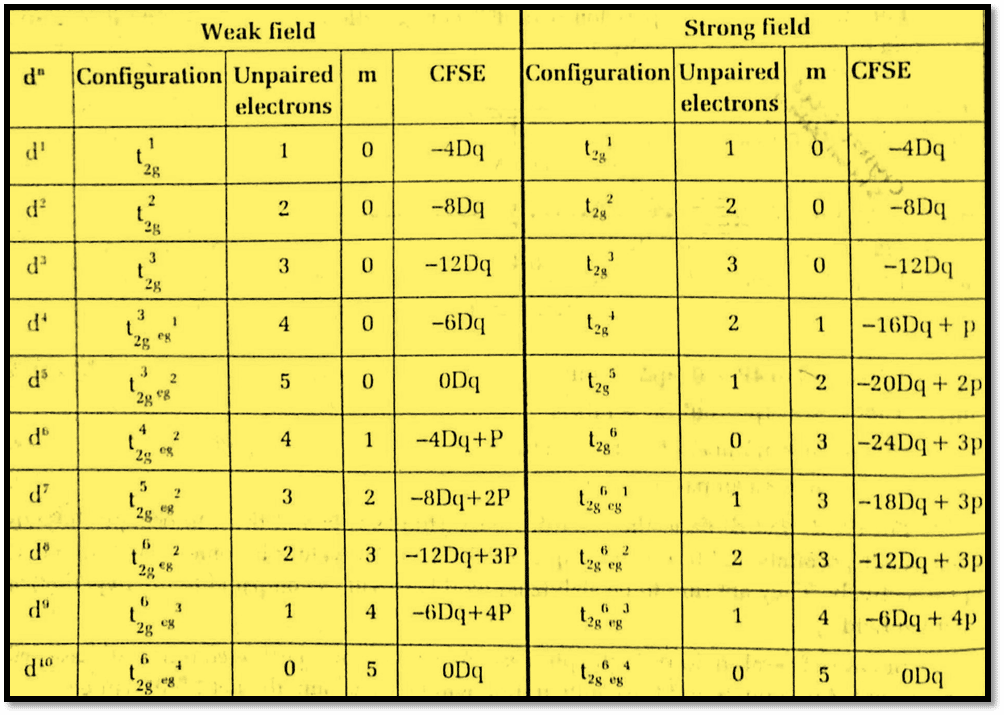
According to Hund’s rule, the electrons in the d1, d2, and d3 cases occupy various degenerate t2g orbitals to stay unpaired. As a result, the CFSE values are 4, 8, and 12 Dq, respectively. They are said to be stabilized to this extent as compared to the hypothetical spherical field.
There are two potential outcomes in the d4 case: either the electron may enter the higher eg or may pair in t2g orbitals. The actual configuration will of course be the lowest energy one and will depend on the relative magnitude of Δo and P. The fourth electron in the d4 case prefers to enter the eg orbital in the presence of a weak field or a high spin state, and the configuration changes to t2g3 eg1, So
CFSE = (3× -0.4 + 1× 0.6) Δo = -0.6Δo = -6Dq
In the case of weak field d5 and d10 cases, the CFSE becomes zero because of the exact balance of stabilization of t2g by eg set. Therefore, subshells that are partially filled and fully filled are spherically symmetric, and no stabilization by the addition of external/additional ligands takes place.
In the case of strong field or low spin cases Δo > P the electrons prefer to stay coupled in the t2g level, whereas the eg level remains unoccupied from d1 to d6 ions. As a result, for strong field cases compared to weak field cases, the CFSEs of complexes with 4 to 7 electrons will be higher.
For example, for the d4 case, the strong field (low spin) configuration will be t2g4 giving CFSE of 1.6Δo (16Dq) as compared to 6Dq (0.6Δo) for the weak field case. But the CFSEs for d8, d9, and d10 cases
are the same irrespective of field strength, which is 12, 6, and 0 Dq respectively. Moreover, crystal field effects for weak and strong octahedral fields are illustrated below:
In the case of tetrahedral complexes, pairing energy is larger than Δt or 10Dq. So electrons enter t2g orbitals as soon as eg orbitals are singly occupied. Therefore, only weak field or high spin cases are considered.
CFSE for d3 tetrahedral case, the configuration is eg2, t2g1.
CFSE = (-0.6q + 0.4P) = (2×-0.6 + 1×0.4) = -0.8Δt = -8Dq
Significance of CFSE
- Determination of complexes crystal structures.
- Prediction of the stabilization of oxidation state.
- It is useful to understand the relative stability of a given complex’s stereochemistry.
- It helps to explain the heat of hydration of transition elements.