Crystal field splitting of d orbitals: Octahedral and Tetrahedral complexes

Crystal field splitting is the separation of five degenerate d-orbitals of metals under the influence of approaching ligands into two sets (t_2g and e_g) having different energy. It takes place under the influence of the electrostatic field of ligand that results in the repulsion between the electrons of metal ions and that of ligands when the ligand approaches towards central metal cation by its negative end. As a result, the degeneracy of orbitals gets destroyed and the splitting of d orbitals takes place into two sets of d-orbitals; e_g and t_2g having different energies.

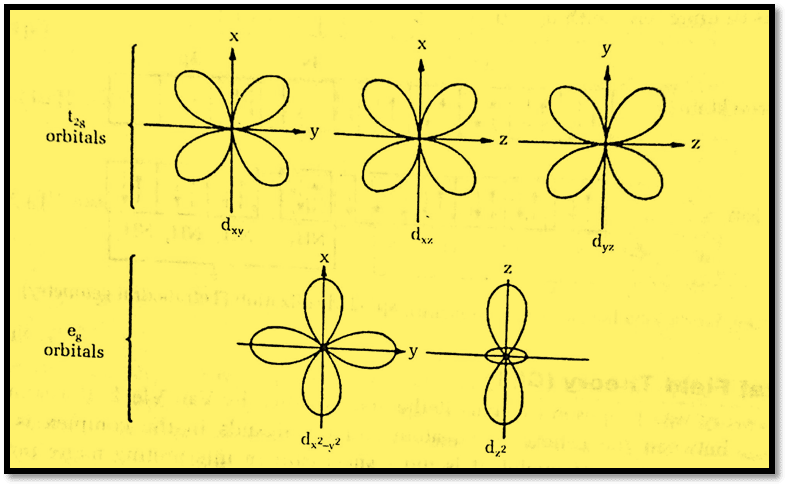
An isolated gaseous metal ion has degenerated (same energy) five d-orbitals. The d-orbitals remain degenerate if a spherically symmetrical field of negative charges surrounds the metal ion, but all of them will gain energy due to repulsion between the negative field and the negative electrons in the orbitals of metal. The symmetry of the field will be destroyed if it is generated by the action of actual ligands, such as anions or the -ve ends of dipolar ligands like NH₃ or H₂O. The core of crystal field theory is this splitting of d-orbital energies and its consequences.

Splitting of d orbitals in Octahedral complexes

Let’s consider the six ligands that are moving toward the metal cation along the coordinate system’s axes to explain octahedral symmetry. Due to negative charge repulsion, all d orbitals will have higher energies than the free ion. All the d-orbitals won’t be affected equally since the field of -ve charge is no longer spherical.

In an octahedral complex, the metal ion is at the center of the octahedron and the ligands are at the six corners. The lobes of eg orbitals (d_x²-y² and d_z²) point along the axes and the lobes of t2g orbitals (d_xy, d_xz, d_yz) point in between the axes. eg orbitals are close to the direction of ligands whereas the t2g orbitals are somewhat farther with respect to the position of the ligands. The orbitals lying along the axes i.e. eg will be more strongly repelled than the orbitals with lobes directed between the axes i.e. t2g.

The d orbitals are now split into two sets of orbitals, one set, eg has higher energy and another set t2g has lower energy as shown below:

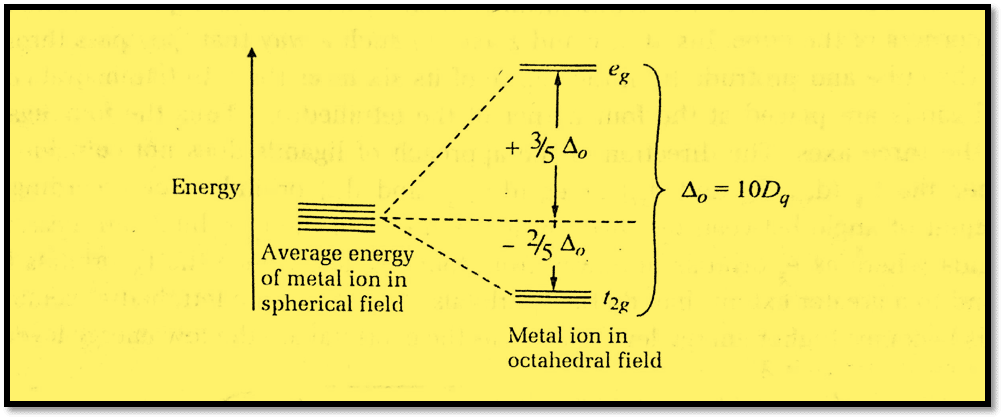
The symbol Δ_o (octahedral) or 10Dq indicates the extent to which the e_g and t_2g orbitals are separated in an octahedral complex. The term “crystal field splitting energy” refers to this Δo or 10Dq. More insight into the nature of this splitting can be obtained by viewing the formation of a complex as the following two-step process:

• In the first step, the ligand approaches the central metal producing a hypothetical spherical field, which repeals all of the d-orbitals to the same extent.
• In the second step, the ligands exert an octahedral field, which splits the orbital degeneracy.

We observe that the orbitals’ “center of gravity” or barycentre does not change as we move from the first to the second step. e_g level is located 0.6 Δ_o or 6 Dq above and t_2g level is located 0.4 Δ_o or 4 Dq below the barycentre in an octahedral field. In order to maintain the center of gravity, the total energy gain of four e_g electrons must equal the total energy loss of six t_2g electrons.

Splitting of d orbitals in Tetrahedral complexes

Tetrahedral symmetry specifies that the four ligands approach the center metal ion through the cube’s four alternate corners. These 4 ligands are therefore situated between the three axes. Due to the fact that the lobes of t_2g orbitals, specifically d_xy, d_xz, and d_yz, point between the x, y, and z axes, these will be more repulsed by ligands than eg orbitals, which point along the x, y, and z axes. In order to stabilize with respect to the barycenter, the energy of the t_2g orbitals is increased while the energy of the eg orbitals is decreased.

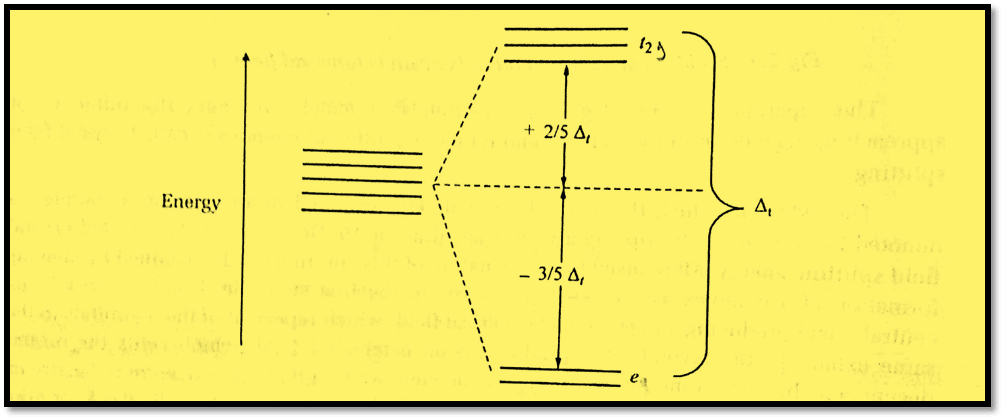
Furthermore, since the center of gravity rule holds, the upper levels are raised by 0.4Δ_t, and the lower ones are stabilized by 0.6Δ_t from the barycenter, giving an energy scheme that is exactly the inverse of that for octahedral symmetry. Due to the tetrahedron’s lack of a center of inversion, the g subscripts that were used for cubic and octahedral fields are no longer appropriate.

Because there are only two-thirds as many ligands as in the case of an octahedral field and because they have a less direct impact on the d orbitals, the magnitude of crystal field splitting in tetrahedral fields is typically smaller than that in octahedral fields. For the identical metal ion, ligands, and metal-ligand distances, the point charge model predicts that Δ_t = (4/9)Δ_o.

In comparison to weak field ligands, strong field ligands result in a larger energy differential between t₂ and e. Tetrahedral splitting, however, is almost generally lower than octahedral splitting. As a result, electron pairing is never energetically advantageous and all tetrahedral complexes are high-spin.

Splitting of d orbitals in square planar complexes

The resulting complex is referred to as being tetragonally distorted if two trans ligands in an octahedron (for instance, those along the z-axis in ML₆) are moved either towards or away from the metal ion so that their distance from the metal cation is slightly greater than that of the other four ligands. Such distortions are typically not preferred since they lead to a net loss of bonding energy. However, a Jahn-Teller effect can favor such a distortion in some circumstances.

The d-orbitals along the z-axis, d_z², d_xz, and d_yz, will experience a decrease in electrostatic repulsions from the ligands and thus be stabilized when the two z ligands are shifted away from their position in an octahedral complex. The “non-z” orbitals will gain energy at the same time while the barycenter stays the same. Overall, the eg level splits into an upper (d_x²–y²) and a lower (d_z²), while the t_2g set splits into a (dxy) and a doubly degenerate eg ( d_xz, and d_yz).

We obtain a square planar geometry if the two trans ligands along the z-axis are totally removed. This is accompanied by a rise in energy of d_x²–y² and d_xy and a reduction in energy of d_z², d_xz, and d_yz).

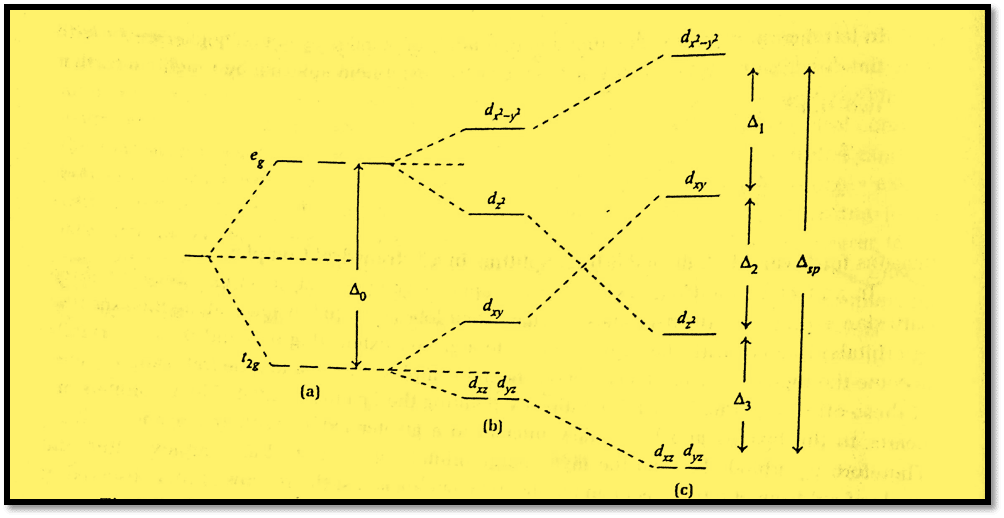
Metal ions in a d8 configuration prefer the square planar geometry when a strong field is present. This is because, this combination gives low spin complexes with 8 d-electrons occupying the low-energy d_xz, d_yz, d_z², and d_xy orbitals, while the high-energy d_{x² -y²} orbital remains unoccupied. The stronger the surrounding field, the higher the d_{x² -y²} orbital will be raised. However, as long as this level is vacant, the complex will stabilize overall since the lower occupied orbitals will reduce the energy by a corresponding amount.

Relative order of orbital energies: Octahedral, Tetrahedral, and Square Planar

The relative order of orbital energies for octahedral, tetrahedral, and square planar complexes are
Δ_sp > Δ_o > Δ_t, where Δsp is the crystal field splitting of the square planar complex.

Δt = (4/9)Δ_o = 0.45Δ_o and Δ_sp = 1.3Δ_o

The difference in value between Δsp and Δo is caused by the fact that in Δsp, the d_xz and d_yz orbitals only interact with two ligands, whereas in Δo, they do so with four ligands.

Compared to octahedral fields, the magnitude of the crystal field splitting, Δ_t, is significantly less. The reason for this is that although in Δ_o ligands lie directly along any axis, in Δ_t no ligands do the same. In addition, Δt has just four ligands while Δ_o has six. Consequently, Δ_t is approximately (2/3) × (2/3) = 4/9 of Δ_o. Since Δ_o>Δ_t,  octahedral complex formation is favored by crystal field splitting.

Crystal Field Splitting Video