Born-Haber Cycle: Determination of Lattice energy

The Born-Haber cycle is a simplified and cyclic method to correlate the lattice energy of ionic crystals with other thermodynamic data which is experimentally determinable. It involves the formation of an ionic compound from the reaction of a metal (often group 1 and 2 elements) with a non-metal.

Since the direct calculation of lattice energy is quite difficult as the required data is often not available, lattice energy is determined indirectly by the use of the Born-Haber cycle. It was named after and developed by two German physical chemists; Max Born and Fritz Haber who first used it in 1919.

Born-Haber cycle calculates the lattice energy by comparing the standard enthalpy of formation of the ionic compound (from the element) to the enthalpy required to make gaseous cations and anions from the element. This is an application of Hess’s law.

How to calculate lattice energy from Born-Haber cycle?

Let us take the formation of one mole of NaCl(s) (MX type salt) from Na(s) and Cl₂(g). The formation of NaCl(s) from two different paths interrelating different thermochemical quantities is shown in the cycle below:

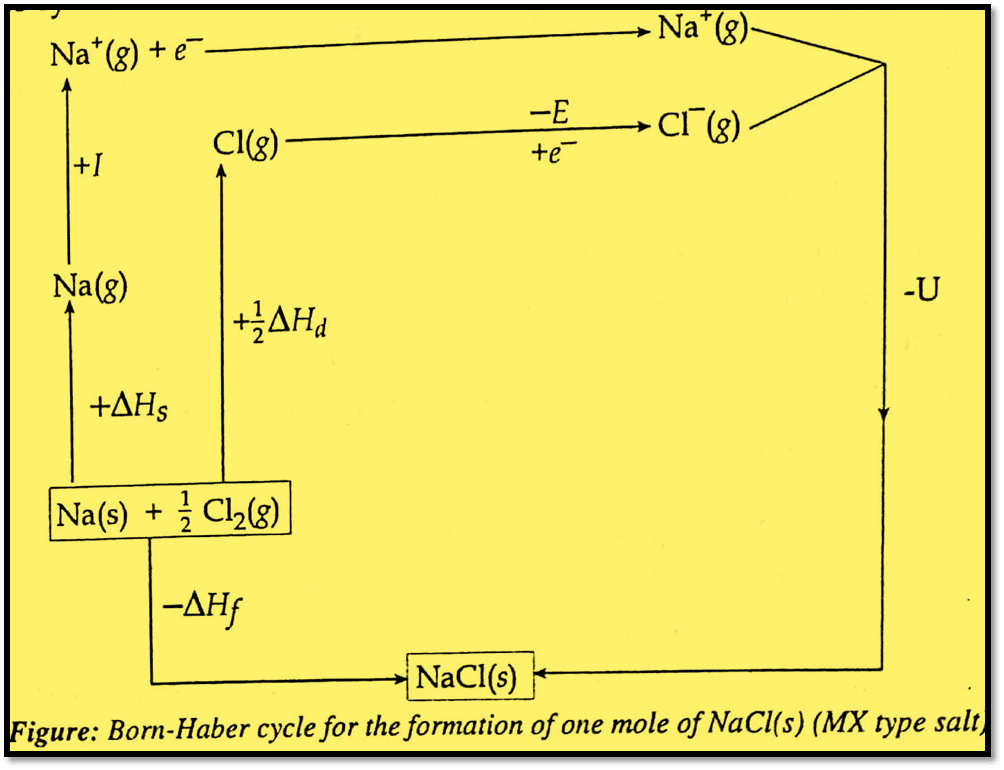
The crystalline NaCl(s) can be formed by either of the following two different processes:

(i) Direct combination of Na(s) and Cl₂(g)

In this process, one mole of Na(s) combines with a half mole of Cl₂(g) to form one mole of crystalline NaCl(s). The energy released in this process is called enthalpy of formation, ΔH_f.

(ii) Indirect method involving the following five steps:

(a) Sublimation of Na(s) into Na(g): Energy required to sublimate Na(s) into Na(g) is called enthalpy of sublimation (ΔH_s).

(b) Ionization of Na(g) into Na⁺(g): Energy required to ionize Na(g) into Na⁺(g) is called ionization energy (I).

(c) Dissociation of Cl₂(g) into Cl(g) atom: Energy required to break the Cl-Cl bond to produce Cl- atoms is called enthalpy of dissociation (ΔH_d).

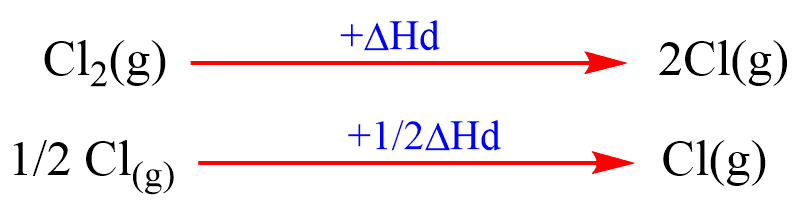
(d) Formation of Cl^–(g): Cl-atom gain an electron to from Cl^–(g) ion. The energy released in such a process is called electron affinity (E).

(e) Combination of Na⁺(g) and Cl^–(g) to form NaCl(s): Gaseous Na⁺ and Cl^– combine to form crystalline NaCl(s). The energy released in this process is called lattice energy(U).

Hess’s law of constant heat of summation states that the energy of the initial state (i.e., reactant) and the final state (i.e., product) in a chemical reaction determines the enthalpy change, but not the path traveled. Applying Hess’s rule, it is clear from the cycle that the enthalpy of formation (ΔH_f) is equal to the algebraic sum of each of the five energy terms, or, in other words, the Born-Haber cycle equation for MX-type salt is

ΔH_f = ΔH_s + I + 1/2 ΔH_d + E + U (For MX type salt)

In the above equation, ΔH_f, E, and U are exothermic terms, and the remaining three ΔH_s, I and ΔH_d are endothermic terms. Therefore taking sign convention, negative for exothermic and positive for endothermic, the equation becomes:

– ΔH_f = ΔH_s + I + 1/2 ΔH_d – E – U (For MX type salt)

The net enthalpy of formation and the first four of the five energy terms can be determined experimentally. Hence lattice energy can be calculated by substituting the other energy terms in the Born-Haber cycle or in the above equation.

Born-Haber cycle for the formation of MX₂-type salt

Let us take the formation of one mole of CaCl₂(s) from Ca(s) and Cl₂(g). The balanced equation for the formation of one mole of CaCl₂(s) is given as:

Ca(s) + Cl₂(g) → CaCl₂(s)

The Born-Haber cycle steps involving the formation of CaCl₂(s) by two different methods are:

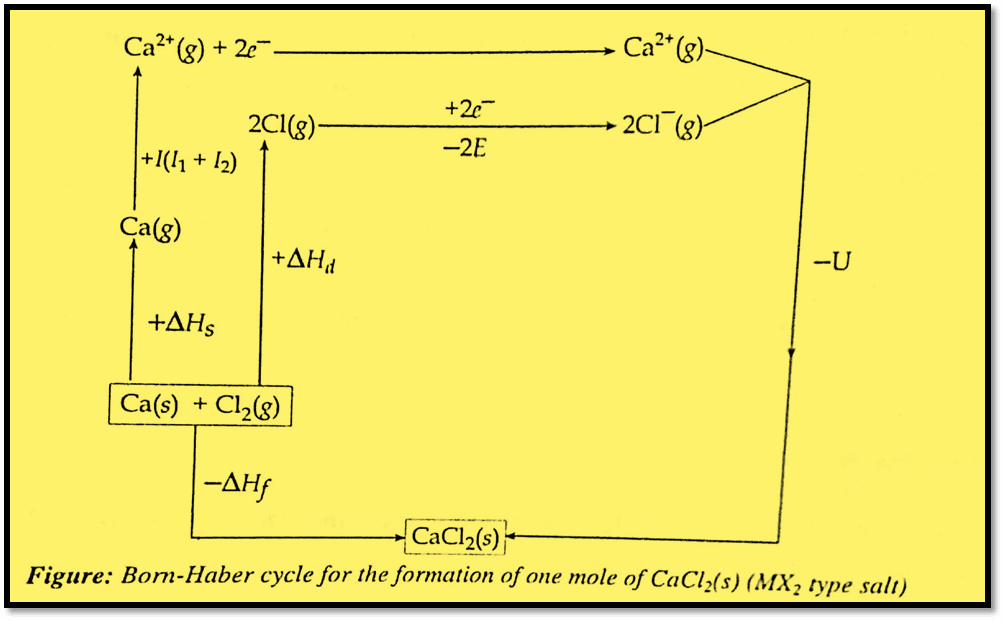
Now, let us apply Hess’s law of constant heat of summation. According to this law, the enthalpy change in chemical reactions depends only on its initial state and final state but not on the route used in the change. Therefore from the Born-Haber cycle, it is clear that

ΔH_f = ΔH_s + I (I₁ +I₂) + ΔH_d + 2E + U (For MX₂ type salt)

Born-Haber cycle for the formation of MX₃-type salt

Let us take the formation of one mole of AlF₃ from Al(s) and F₂(g). The balanced equation for the formation of one mole of AlF₃ is:

Al(s) + 3/2 F₂(g) → AlF₃(s)

The formation of AlF₃(s) in two different ways is shown in the Born-Haber cycle:

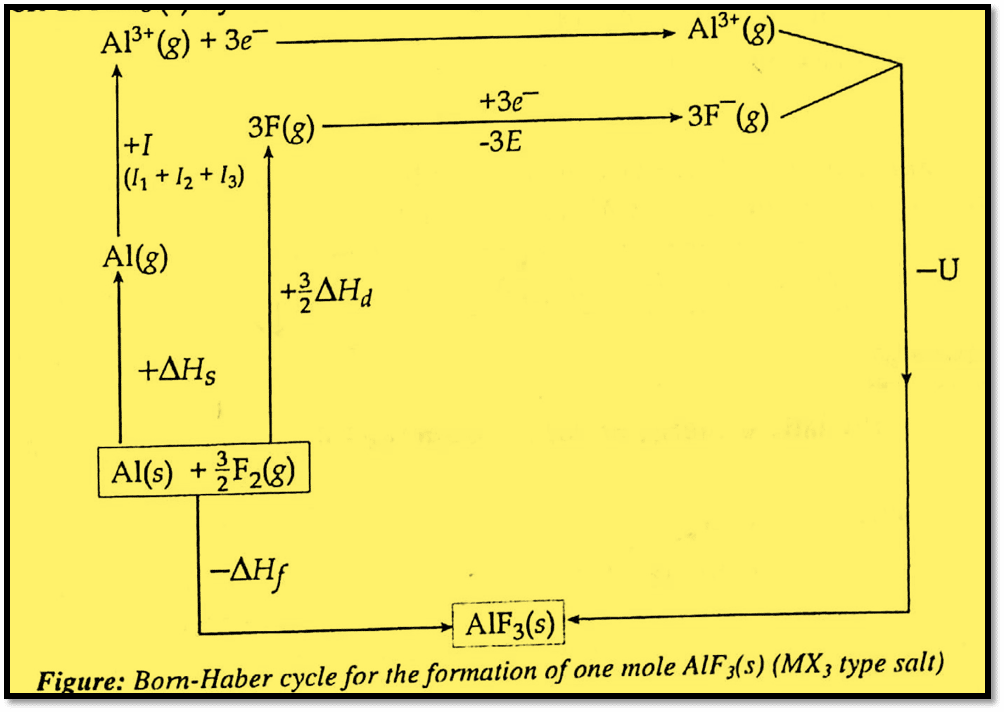
Now, applying Hess’s law of constant heat of summation, the equation for enthalpy of formation for one mole of AlF₃(s) is given as:

ΔH_f = ΔH_s + I (I₁ +I₂ +I₃) + 3/2 ΔH_d + 3E + U (For MX₂ type salt)

Application of Born-Haber Cycle

• Stability of compounds: If different thermochemical data for a compound are substituted in the Born-Haber cycle, it will help to rationalize the existence of certain compounds and the non-existence of others. Moreover, it determines the stability of the compounds.
• Estimation of electron affinities: From theoretical lattice energy, the Born-Haber cycle can be utilized to calculate the electron affinities of individual atoms. However, atoms can only be estimated to have a first electron affinity. The inter-electronic repulsion between the anion and extra electrons causes an issue in second electron affinity calculations. The first and second E.A. can be determined, though.
• Estimation of enthalpy of formation: One of the energy terms used in the Born-Haber cycle is the enthalpy of formation. If the other energy terms of the cycle are known, they can be calculated from this cycle.
• The lattice energy values are negative, indicating that crystallization is exothermic and that the crystal is more stable than its constituent ions.
• The stability of ionic compounds would increase as the lattice energy value increased. When the lattice energy is large, the electrostatic attraction between the cation and anion is also strong. Because of this, ionic compounds with high lattice energy will also have high melting points, boiling points, enthalpy of formation, and enthalpy of sublimation.

Born-Haber Cycle Video