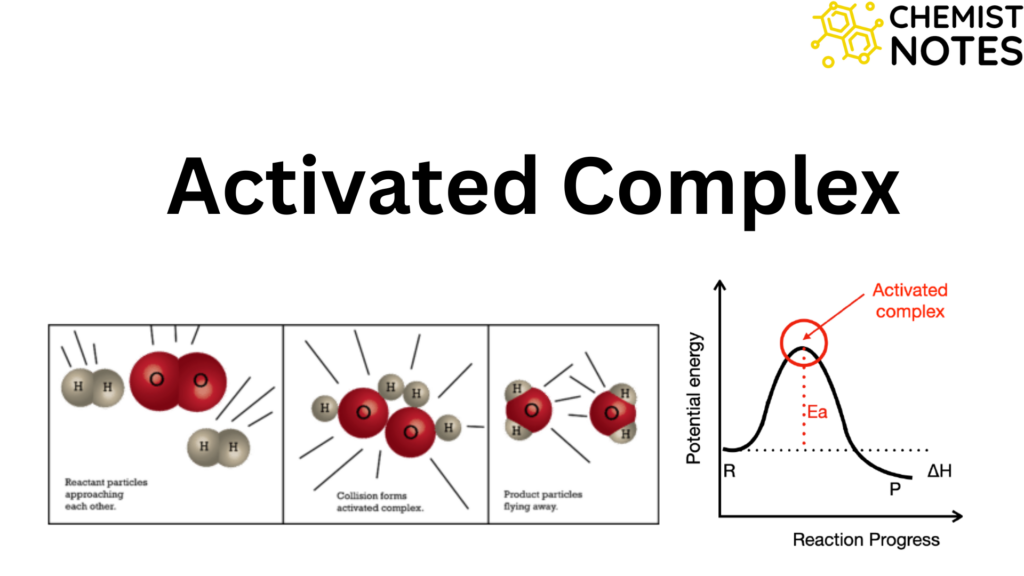
Table of Contents
ToggleThe lattice energy of an ionic solid is a measure of the strength of the bond in that ionic compound. Several properties like volatility, solubility, hardness, and so on can be predicted using lattice energy. It is used to explain the stability of ionic solids. However, lattice energy (U) cannot be determined directly, but experimental value can be estimated using the Born-Haber cycle.
What is lattice energy?
Lattice energy is defined as the amount of energy released when cations and anions are brought from infinity to their respective lattice side in a crystal to form one mole of the ionic solid. The formation of a mole of ionic solid from the constituent gaseous ions may be represented by “U”.
M+(g) + X–(g) → M+X–(s) +Energy released called lattice energy
[Note: Lattice energy ‘U’ has a negative sign since energy is released in the process].
The lattice energy of an ionic compound is also defined as the amount of energy required to break one mole of ionic compounds into cations and anions in the gaseous phase separated by an infinite distance.
M+X–(s) +Energy released called lattice energy → M+(g) + X–(g)
[Note: U has a +ve sign since energy is absorbed in this process].
Calculation of lattice energy
The phrase ‘how to calculate lattice energy’ is the most common query that we face when we talk about lattice energy. Here are the ways regarding the calculation of lattice energy.
The lattice energy of an ionic solid can be calculated theoretically on the basis of coulomb interaction between the ions present in the crystals. There are two types of interactions:
1. Attractive interaction between oppositely charged ions
The potential energy of a pair of ions of opposite charges varies inversely at the distance ‘r’ between the ions. This may be expressed as
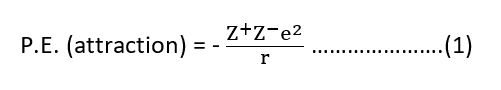
where Z+ and Z– are the charges of the +ve and -ve ions, ‘e’ is the charge on an electron and ‘r’ is the inter-ionic distance.
For more than two ions, the electrostatic energy depends on the number of ions, and also on their arrangement in space. For one mole, the attractive energy is
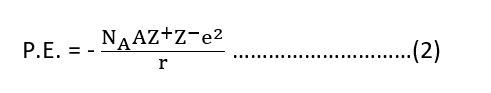
where NA is the Avogadro constant and A is the Madelung constant which depends on the geometry of the crystal.
2. Repulsive interactions between due to interpenetration of electron clouds
As a cation and an anion come very close to each other, there is repulsion between them because of the interpenetrating of electron clouds. The potential energy due to their repulsion is
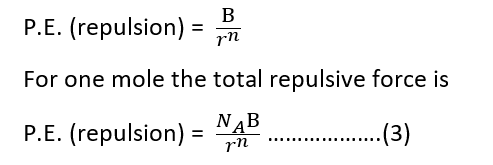
where B is constant, known as the repulsion coefficient and n is called the Born exponent. The total energy holding the crystal together is lattice energy ‘U’.
Since U = P.E. (attraction) + P.E. (repulsion)
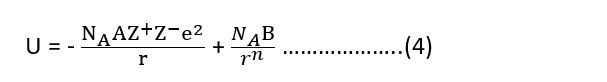
The equilibrium distance between ions is determined by the balance between attractive and repulsive terms. At equilibrium,
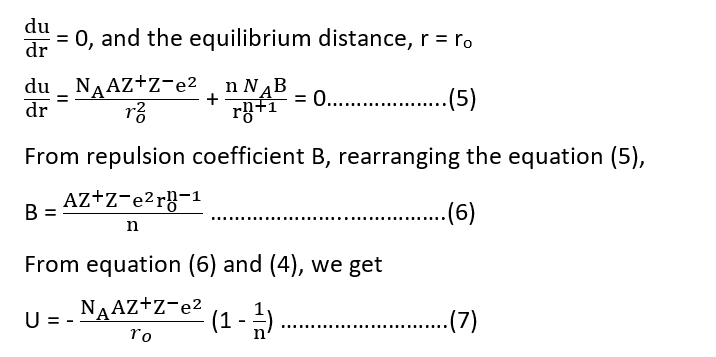
Equation 7 is called the Born-Lande equation. Using SI units, the equation takes the form:
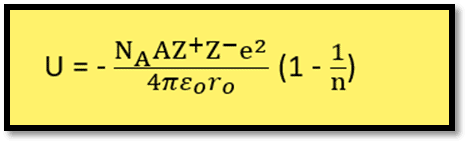
Factors affecting lattice energy
Some of the important conclusions regarding the factors affecting lattice energy can be made considering the Born-Lande equation
- Lattice energy is directly proportional to the product of charges (Z+Z–) on ions: The value of lattice energy would increase with increasing cation and anion charges, which would also increase the stability of the ionic crystal.
- Lattice energy is inversely proportional to the interionic distance: The smaller the inter-ionic distance (sum of the radius of cation and anion), the greater would be the magnitude of lattice energy and therefore greater would be the stability of the ionic compound.
- The lattice energy is directly proportional to the value of Madelung constant ‘A’
- The higher the value of Born exponent ‘n’, the greater would be the value of lattice energy.
Importance of lattice energy
Lattice energy is an important parameter for ionic solids in order to explain the following properties of ionic compounds.
- Stability of ionic compounds: Stable ionic compounds have high lattice energy. In the context of this, if lattice energy is high, properties such as melting temperature, boiling point, enthalpy of formation, and enthalpy of sublimation would be high.
- Solubility of ionic compounds: When the solvation energy is higher than the lattice energy, the ionic compounds are soluble in the solvent. The salt remains insoluble in the solvent if the lattice energy is higher than the solvation energy. This fact allows us to understand why alkaline earth metal salts are insoluble in water.
- Structure of ionic compound: The radius ratio rule only offers a general overview of the geometrically possible shapes of ionic compounds. The radius ratio rule sometimes predicts the incorrect structure. The lattice energy is one of the most significant factors that affect this rule. The ionic compound will adopt that structure which would give the most favorable lattice energy