Table of Contents
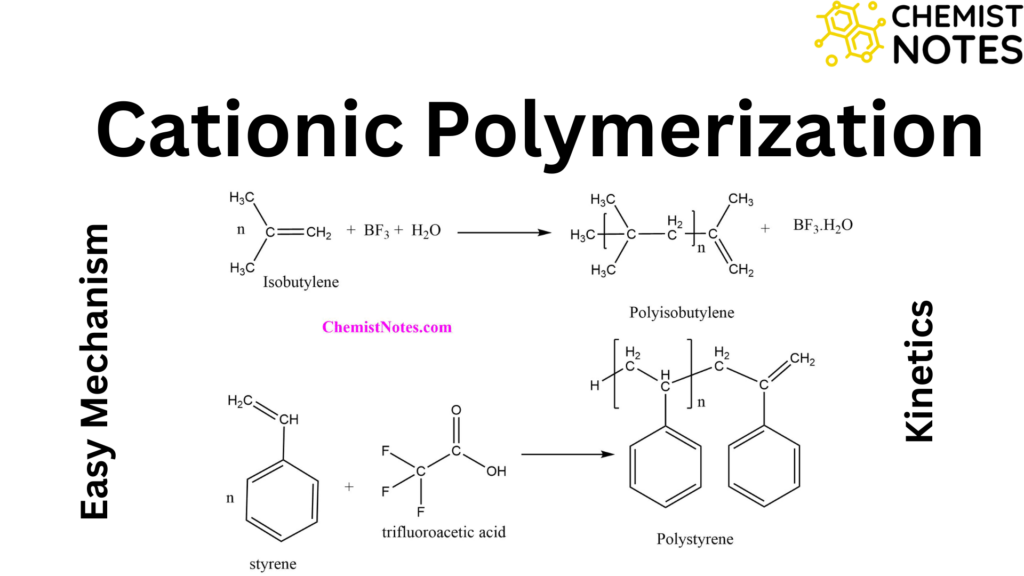
ToggleThe Carnot cycle is a hypothetical, ideal, and reversible cycle process suggested by french engineer Sadi Carnot in 1824 to show the greatest possible conversion of heat into work. An ideal machine to demonstrate this cycle is called the Carnot heat engine. Carnot demonstrated that work done in a carnot cycle is maximum as the various phases involved are reversible and hence reversible work is maximum.
Carnot Heat engine
The Carnot heat engine is a machine by which a working substance can interchange mechanical work with its surroundings and can exchange heat with two reservoirs, one at high temperature (the source), and the other at a lower temperature (the sink). It consists of a cylinder fitted with an ideal piston and contains a mole of an ideal gas as the working substance.
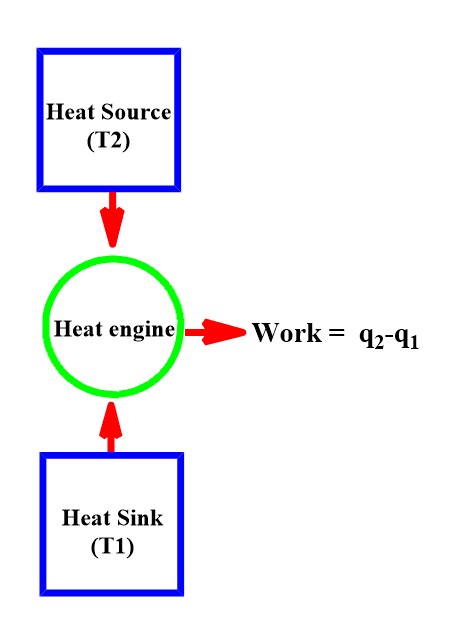
In this cycle, the working substance returns back to the initial state after undergoing a certain operation. Four operations are involved in the cycle, two of which are carried out isothermally and the other two adiabatically.
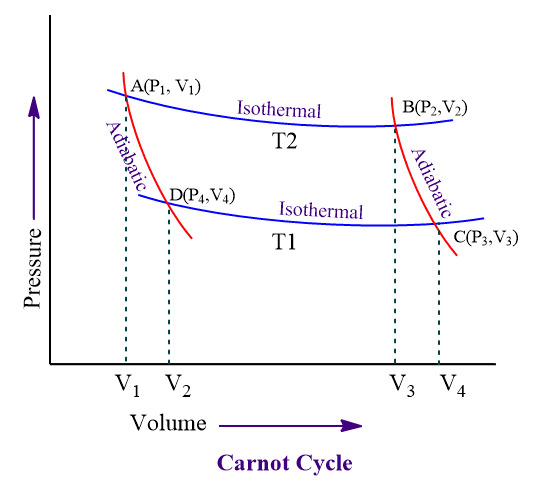
Consider 1 mole of gas in a cylinder fitted with a frictionless and weightless piston. The gas is then subjected to a series of four steps:
Step I: Isothermal reversible expansion at temperature T2
The cylinder is placed on the source and the piston is moved very slowly. The gas is now allowed to expand reversibly and isothermally at temperature T2, so that the volume increases from V1 to V2 (i.e. point A to B as shown in the above figure)
From the first law,
△E = q – W
△E = 0 (for isothermal process)
q = W
i.e. heat absorbed is equal to the work done by the system on the surrounding.
Let q2 be the heat absorbed by the system at temperature T2 and WAB be the work done by the system surroundings. Then,
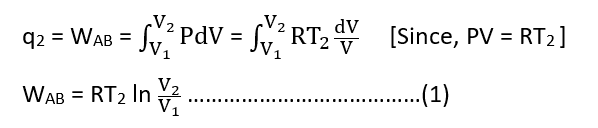
Step II: Adiabatic reversible expansion
The cylinder is now taken out of the source and isolated completely. The gas is then allowed to expand reversibly and adiabatically from volume V2 to V3 (from point B to C in the above figure). Since the work has been done by the system adiabatically, no heat is absorbed (q=0) causing the temperature of the system fall from T2 to T1. Thus, work done on the system by the surrounding, WBC is given by:
△E = q – W
or, △E = -WBC
or, -WBC = CvdT [ ∴ △E = CvdT = Cv(T1 – T2)]
or, -WBC = Cv(T1 – T2)
or, WBC = Cv(T2 – T1) …………………………………(2)
Step III: Isothermal reversible compression at temperature T1
Now, the cylinder is removed from the insulator and transferred to the heat reservoir (sink) at low temperatureT1. The gas is then compressed isothermally and reversibly so that the volume changes from V3 to V4 (point C to D).
For isothermal process,
△E = 0
when q1 amount of heat is given out by the gas to the sink and WCD amount of work is done on the gas by the piston at constant temperature T1. Then,
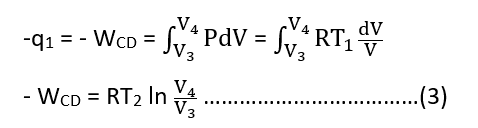
Step IV: Adiabatic reversible compression
The cylinder is removed from the heat sink and is insulated. The gas is then compressed adiabatically and reversibly from volume V4 to V1 (from D to A) and the temperature is changed from T1 to T2. Since, no heat is evolved or absorbed, q=0 and work done on the gas, WDA is given by
WDA = △E = Cv(T1 – T2) = -Cv(T2 – T1)
-WDA = -Cv(T2 – T1)………………………………(4)
The net work done in the cyclic process,
W = WAB + WBC -WCD -WDA
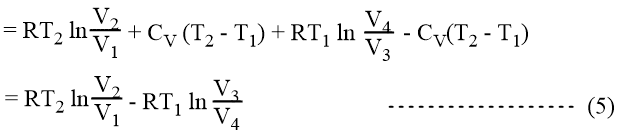
Since V3 and V4 are related to V1 and V2 as
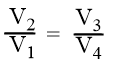
Now from equation (5),
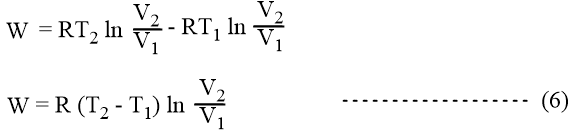
The net heat absorbed (Q) in the cyclic process,
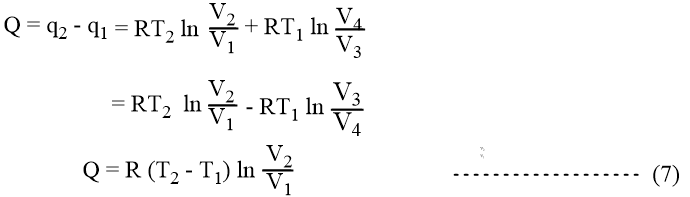
From equations (6) and (7) it can be figured that
W = Q
Hence, the heat absorbed by the gas is equal to the work done by it, which is in concurrence with the first law of thermodynamics.
Efficiency of a Carnot cycle
A machine or an engine is a device that can convert heat into work. Thermodynamically efficiency (ɳ) of a heat engine is defined as the ratio of work produced to the heat supplied, i.e.,
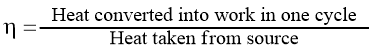
From the above-shown Carnot cycle, tet the amount of heat absorbed from the source (at a temperature T2) be q2, the amount of workdone be W, and the amount of heat rejected to the sink (at temperature T1) be q1. Then,

But we have seen that, W = q = q2 – q1
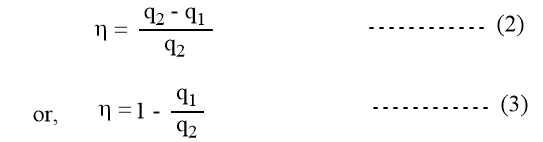
Since W = R (T2-T1) ln V2/V1
and, q2 = RT2 ln V2/V1
Equation 1 can also be written as,
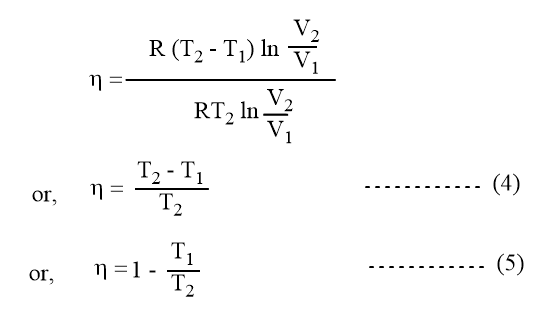
Combining equations 2 and 4 we get,
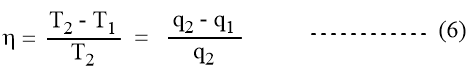
The following conclusion has been made from the above equation:
- ɳ depends upon the temperature difference T2 – T1. The higher the difference between the temperature of source and the sink, the greater will be the efficiency of the engine.
- If T1 = 0, the value of ‘ɳ’ is equal to one. This implies that W = q2, i.e., entire heat is converted into work. Thus, if the engine works between absolute zero and a higher temperature, complete conversion of heat into work may be possible. But as absolute zero cannot be realized in actual practice, therefore, no heat engine can be constructed whose efficiency is unity or 100% i.e., heat cannot be transformed completely into work.
- When T1=T2, the value of ‘ɳ’ is zero and consequently W is also equal to zero. It means no work can be produced when the engine operates under isothermal conditions.