Table of Contents
ToggleSlater’s rule is used to estimate the effective nuclear charge experienced by an electron in different atomic orbitals. These rules are based on the experimental data for electron promotion and ionization energies.
Slater’s Rule states that the net charge experienced by an electron is equal to the charge expected from a given number of protons minus the net charge from other electrons. Using the actual number of protons in the nucleus and the effective shielding of electrons in each orbital “shell” (for example, to compare the effective nuclear charge and shielding 3d and 4s in transition metals), one can estimate the effective nuclear charge Zeff using Slater’s rules. Predictions of properties like electron configurations and ionization energies can be performed with relative ease using Slater’s rules.
How to calculate effective nuclear charge using Slater’s rule
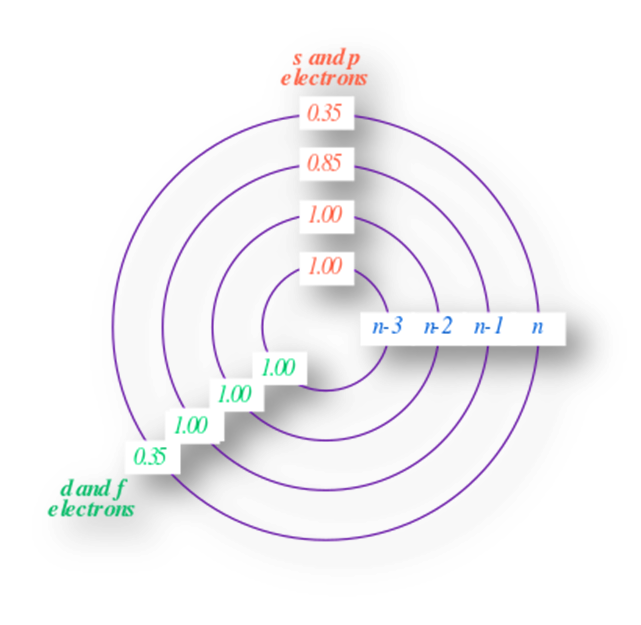
Some of the most important rules for determining the effective nuclear charge using slater’s rules are as follows:
- For ns or np orbitals on valence shell
- Zero contribution of the σ for the electron under consideration.
- 0.35 value of σ for each remaining electron present on the valence shell.
- 0.85 values of σ for each electron present in the penultimate i.e. (n-1)th shell.
- 1 value of σ for each electron present in the next inner shells.
- If σ is calculated for the electrons in 1s orbital then the electron contributes 0.30 value for σ.
- For (n-1)d orbitals
- Zero values of σ for the electrons present in the ns orbital on the valence shell.
- 0.35 value of σ for the electrons present in the (n-1) d orbital.
- 1 value of σ for the (n-1)s, (n-1)p, and all other inner electrons
- σ for (n-1) d electrons = 0.35 × number of (n-1) d electrons + 1 × number of all remaining inner electrons.
Slater’s Rule Examples
1.σ and Zeff for 1s electrons in He atom
He = 1s2
σ = 0 + 1 × 0.30 (σ for one valence electron = 0) = 0.30
Zeff = Z – σ = 2 – 0.3 = 1.7
2. σ and Zeff for 4s electrons in Na-atom (Z = 11)
| Na = 1s2 | 2s22p6 | 3s1 |
| Inner shell | Penultimate shell | Valence shell |
| = total 2 electrons | = total 8 electrons | = total 1 electron |
| σ value for each penultimate shell electrons= 1 | σ value for each valence shell electrons = 0.85 | σ = 0 |
σ = 2 × 1 + 8 × 0.85 + 0
= 2 + 6.80 = 8.80
Therefore, Zeff = Z – σ = 11 – 8.8 = 2.2
3. σ and Zeff for 4s electrons in Fe-atom (Z = 26)
| Na = 1s22s22p6 | 3s23p63d6 | 4s2 |
| Inner shell | Penultimate shell | Valence shell |
| = total 10 electrons | = total 14 electrons | = total 2 electrons |
| σ value for each penultimate shell electrons= 1 | σ value for each valence shell electrons = 0.85 | σ = 0.35 |
σ = 10 × 1 + 14 × 0.85 + 0.35 + 0
= 10 + 11.9 + 0.35 = 22.25
Therefore, Zeff = Z – σ = 26 – 22.25 = 3.75
4. σ and Zeff for p-electrons of valence shell in O-atom (Z = 8)
| O = 1s2 | 2s22p4 |
| penultimate shell | valence shell |
| = total 2 electrons | = total 6 electrons |
| σ value for each penultimate shell electrons= 0.85 | σ value for each valence shell electrons = 0.35 |
σ = 2 × 0.85 + 5 × 0.35 + 0 (σ = 0 for 1 valence electron)
= 1.7 + 1.75 = 3.45
Therefore, Zeff = Z – σ = 8 – 3.45 = 4.55
5. σ and Zeff for p-electrons of valence shell in F-atom (Z = 9)
| F = 1s2 | 2s22p5 |
| penultimate shell | valence shell |
| = total 2 electrons | = total 7 electrons |
| σ value for each penultimate shell electrons= 0.85 | σ value for each valence shell electrons = 0.35 |
σ = 2 × 0.85 + 6 × 0.35 + 0 (σ = 0 for 1 valence electron)
= 1.7 + 2.10 = 3.80
Therefore, Zeff = Z – σ = 9 – 3.80 = 5.2
6. σ and Zeff for p-electrons of valence shell in Cl-atom (Z = 17)
| Cl = 1s2 | 2s22p6 | 3s23p5 |
| Inner shell | Penultimate shell | Valence shell |
| = total 2 electrons | = total 8 electrons | = total 7 electrons |
| σ value for each penultimate shell electrons= 1 | σ value for each valence shell electrons = 0.85 | σ value for each valence shell electrons = 0.35 |
σ = 2 × 1 + 8 × 0.85 + 6 × 0.35 + 0 (σ = 0 for 1 valence electron)
= 2 + 6.80 + 2.10 = 10.90
Therefore, Zeff = Z – σ = 17 – 10.90 = 6.10
7. σ and Zeff for 3d electrons in Cr-atom (Z = 24)
| Cr = 1s22s22p63s23p6 | 3d5 | 4s1 |
| = total 18 electrons | = total 5 electrons | = total 1 electron |
| σ value for each penultimate shell electrons= 1 | σ value for each valence shell electron = 0.35 | σ = 0 |
σ = 18 × 1 + 4 × 0.35 + 0 + 0 (σ = 0 for 1 electron in 3d orbital)
= 18 + 1.40 = 19.40
Therefore, Zeff = Z – σ = 24 – 19.4 = 4.6
8. σ and Zeff for 3d electrons in Zn-atom (Z = 30)
| Zn = 1s22s22p63s23p6 | 3d10 | 4s2 |
| = total 18 electrons | = total 5 electrons | No contribution |
| σ value for each penultimate shell electrons= 1 | σ value for each valence shell electron = 0.35 | σ = 0 |
σ = 18 × 1 + 9 × 0.35 + 0 + 0 (σ = 0 for 1 electron in 3d orbital)
= 18 + 3.15 = 21.5
Therefore, Zeff = Z – σ = 30 – 21.5 = 8.5
Application of Slater’s Rule
- The effective nuclear charge of a multi-electron atom can be calculated using Slater’s rules.
- Slater’s rule of effective nuclear charge explains why the 4s orbital is filled before the 3d orbitals, in K and Ca.
- The concept of effective nuclear charge explains the variation of atomic radius, ionization energy, electronegativity, etc. in the periodic table.
- It also explains why the radius of the cation is smaller than the parent neutral atom and why the radius of the cation decreases with an increase in the number of positive charges.
- It also explains why the radius of the anion is larger than the parent neutral atom and why the radius of the anion increases with an increase in the number of negative charges.