Radius Ratio: The radius ratio rule

The ratio of the radius of a cation (r⁺) and the radius of an anion (r^–) is known as the radius ratio (r⁺/r^–). The structure of many ionic solids can be accounted by analyzing the relative sizes of the positive and negative ions. We may use simple geometric calculations to determine how many ions of a particular size can be in contact with a smaller ion. As a result, we can predict the coordination number based on the ion sizes. The crystal structures are determined by the coordination numbers of the ions. Using the radius ratio, we can predict the coordination number and structure of ionic crystals. Among crystals, coordination numbers of 3,4,6,8 are common.

Radius ratio rule

When the coordination number is 3 in an ionic compound AX, 3 X^– ions are in contact with one A⁺ ion. A limiting case arises when the X^– are in contact with one another. By simple geometry, this gives the ratio (radius A⁺/radius X^–) = 0.155. This is the lower limit for a coordination number of three. If the radius ratio is less than 0.155, then the positive ion is not in contact with the negative ions, and it rattles in the holes, and the structure is unstable. As the differences in the sizes of the ions increase, the radius ratio also increases.

The corresponding limiting radius ratio values for coordination numbers 2, 3, 4, 6, and 8 are:

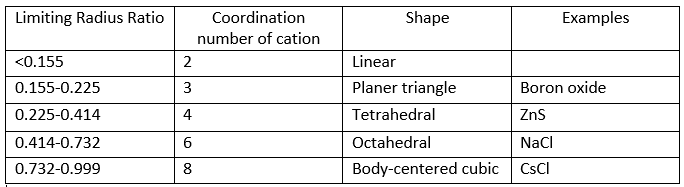
The radius ratio is rarerly 1; in such a case the coordination number is 12.

Calculation Of Some Limiting Radius Ratio Values

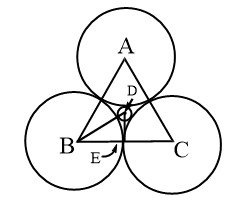
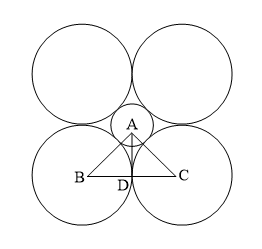
Coordination number 3 (planar triangle)

The smaller positive ions with radius r+ interacted with 3 larger negative ions with radius r-. Plainly AB=BC=AC=2r^–, BE=r^–, BD=r⁺ + r^–, the angle D-B-E is 30^o.

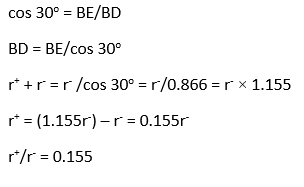
Coordination number 4 (tetrahedral)

Tetrahedral arrangement inscribed in a cube. The angle ABC is the tetrahedral angle of 109^o28′ and hence the angle ABD is half of this, that is 54^o.44′. In the triangle ABD:

Coordination number 6 (octahedral)

The smaller positive ion of radius r+ touches six larger negative ions of radius r-. In the triangle ABD

Limitation of radius ratio rule

• The radius ratio rules can only be used to estimate the cation’s coordination number, not the anion’s.

• They can only be used successfully on crystals of the AB type, which have a cation and an anion in their formula. The rules cannot be applied well to A2B or AB2 crystals.

• In actuality, the extremely high coordination number expected by these laws does not occur in practice.

• The rules are applicable only to crystals made up of ions, that too only when ionic radii are known accurately.