Table of Contents
ToggleZero-order reaction is one of the most studied topics in chemical kinetics. The definition, integrated rate equation, unit of rate constant, characteristic, example, and graphical representation of zero-order reaction are discussed here.
Definition of zero order reaction
If the rate of a reaction is independent of the concentration of reactants, then such a reaction is called a zero-order reaction. The zero-order reaction can be defined as those reactions in which rate is dependent on the zeroth power of concentration term of reactant. The rate of reaction remains the same throughout the reaction in such a zero-order reaction.
How to identify zero order reaction?
It is easy to identify zero-order reactions by studying the rate of reaction. These reactions have a constant rate throughout the reaction. By changing the reactant concentration, the rate is measured and if the rate is found to be constant in each concentration, then the reaction is said to be a zero-order reaction.
zero order reaction integrated rate law
The derivation of the integrated rate law equation of zero-order reaction can be done by considering a general chemical reaction.
Let us consider a reaction,
A→ product
Since the rate of zero order reaction is directly proportional to the zeroth power of concentration of reaction, we can write the rate law expression as,
Rate=dx/dt ∝ [A]0
dx/dt=k[A]0
dx/dt=k
dx=kdt ……………………………………………………………….(1)
On integration of equation (1), we get,
∫dx=k∫dt
x=kt + c …………………………………………..(2)
where c is an integration constant whose value can be determined by using the initial condition i.e. t=o and x=0, we get the value of c=0. Using this value, equation(2) becomes
x=kt…………………………………………………………………(3)
This is the mathematical expression of the integrated rate law equation of zero-order reaction.
Unit of zero order reaction
From integrated rate law expression,
x=kt
k=x/t……………………………………………….(4)
This is an expression of the rate constant of the zero-order reaction.
Using this expression, the unit of rate constant for zero-order reaction can be determined as:
k=(molL-1/sec)=molL-1sec-1
Unit of zero-order reaction: molL-1sec-1 , mol dm-3 sec-1
Half-life time of zero order reaction
This topic has been discussed on a different page.Click here to read.
Zero order reaction example
Some zero-order reaction examples are listed below:
A. Phtochemical reaction:
A photochemical reaction between the H2 and Cl2 in presence of light is an example of zero-order reaction.
H2+Cl2→ 2HCl (in presence of light)
B. Decomposition of N2O
Decomposition of N2O in the presence of Pt- catalyst.
2N2O → 2N2 + O2
Zero order reaction graph/Graphical representation of zero order reaction
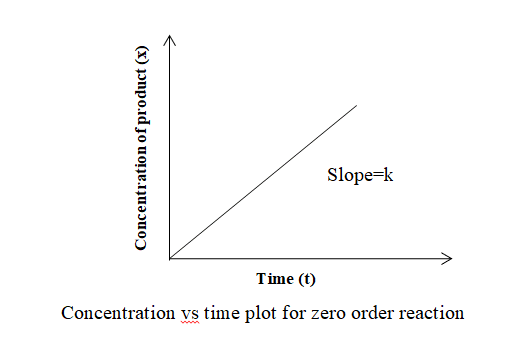
The concentration vs time graph for zero-order reaction is shown below:
When the concentration of product (x) is plotted against time (t), a straight line passing through the origin and having a slope equal to k (rate constant) is obtained.
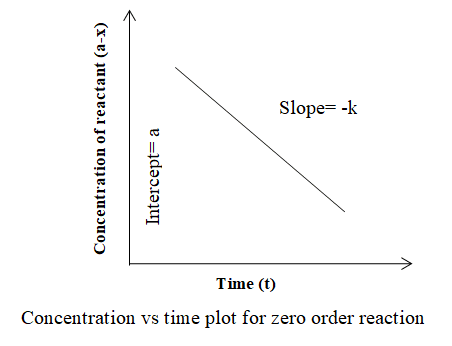
Alternatively, the concentration of reactant (a-x) can be plotted against time (t) and a straight line is obtained as shown below. In this case, the slope is -k and the intercept is a.
Characteristics of zero order reaction
The main characteristics of zero-order reaction are listed as:
- The rate of zero-order reaction is independent of the concentration of reactant.
- The plot of concentration of product (x) vs time (t) is a straight line having slope equal to k.
- The half life time of zero order reaction is directly proportional to the initial concentration of reactant (a).
Zero order reaction video
FAQs:
what is zero-order reaction?
Zero-order reaction can be defined as those reactions in which rate is dependent on the zeroth power of concentration term of reactant.
what is the unit of zero-order reaction?
The Unit of zero-order reaction is molL-1sec-1 , mol dm-3 sec-1