Hittorf Number or Transference Number

Hittorf number, hittorf’s transference number, transference number, or transport number, all terms represent the same meaning. As we know, during electrolysis current is carried by anions and cations. This number gives an idea about how much of the total current is being carried by a particular ion, that be my cation or anion.

Hittorf Number

We know that when an electric current is transmitted through an electrolytic solution, the concentration of the solution changes at the two electrodes. The electricity is carried out by both types of ions. The quantity of electricity carried out by each ion is directly proportional to the speed of that ion.

It means the amount of electricity carried by anions is directly proportional to the speed of anions. Similarly, the amount of electricity carried by cations is directly proportional to the speed of cations. Therefore, the total amount of electricity carried is directly proportional to the sum of the speed of both cation and anions.

Thus, the transport number of an ion is defined as the fraction of the total current carried by that ion.
It is also called transference number or Hittor’s number and is represented by t.

If t+ and t_ be the transport numbers of cation and anion respectively then,

In another word, if the v+ represents the speed of migration of cation and v- that of anion then,

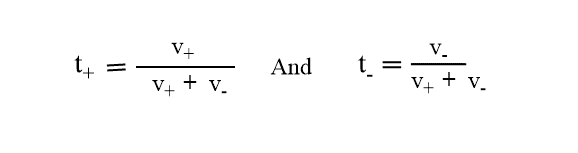
Keep in mind, that the sum of the transport number of cation and anion is always equal to one. Therefore, if the transport number of one ion is known. then that of the other can be calculated.

Moreover, it is possible to determine the value of the transport number of a particular ion experimentally. The two popular methods for the determination of it are:

1. Hittorf’s method (based on hittorf rule)

1. Moving boundary method

Relationship between Equivalent ionic conductance and Transport Number

We know the equivalent ionic conductance of an ion is directly proportional to its ionic mobility. Mathematically, it can be represented as:

λ₊= Fu₊ …………………..(i) and

λ_–= Fu_ ……………………..(ii)

where u₊= ionic mobility of cation at infinite dilution,

u_–= ionic mobility of anion at infinite dilution, and K= proportionality constant

Since 1 gram equivalent of an ion carries one faraday of electricity under unit potential gradient, we can write, K=96500=F

So, the above equations become,

λ₊= Fu₊ …………………….(iii) and

λ_–= Fu_ ……………………….(iv)

From kohlrausch’s law,

Λ_o=λ₊ + λ_–

Λ_o= F(u₊ + u_–) …………………(v)

Dividing equation (iii) by (v), we get

λ₊/ Λ_o = [ u₊/(u₊ + u_–)]= t₊

λ₊=t₊Λ_o

similary, λ_–=t_–Λ_o

These are required relations, mainly useful for solving numerical problems.

Transport Number youtube video

References:

1. Arun Bahl, B. S. Bahl & G. D. Tuli, Essentials of Physical Chemistry, S. Chand and Company Ltd., New Delhi, 2012