Helmholtz-Perrin Model of Electrical Double layer: Easy explanation, 4 failures

The Helmholtz-Perrin model, given by two Scientists Helmholtz and Perrin, is popularly known as the Parallel plate condenser model. The statement, mathematical equation, and failure of this model have been discussed in this blog.

Helmholtz-Perrin model

According to the Helmholtz-Perrin model, the charge on the metal would be induced from randomly dispersed ions in the solution. Thus, the counter layer of a charge of an opposite sign will be developed on metal.

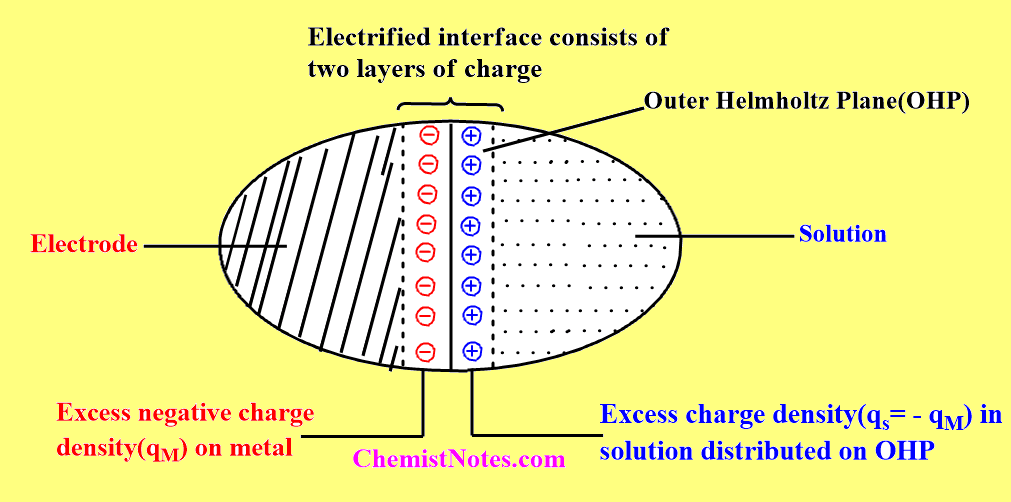
In this way, the electrified interface will consist of two sheets of charge, one on the electrode and the other in the solution. Therefore, it is known as an electrical double layer. Moreover, the charge densities on the two sheets are equal in magnitude but opposite in sign exactly the same as in a parallel plate capacitor, hence also known as a Parallel plate condenser model. The potential between these two layers of charge drops linearly as shown in the figure.

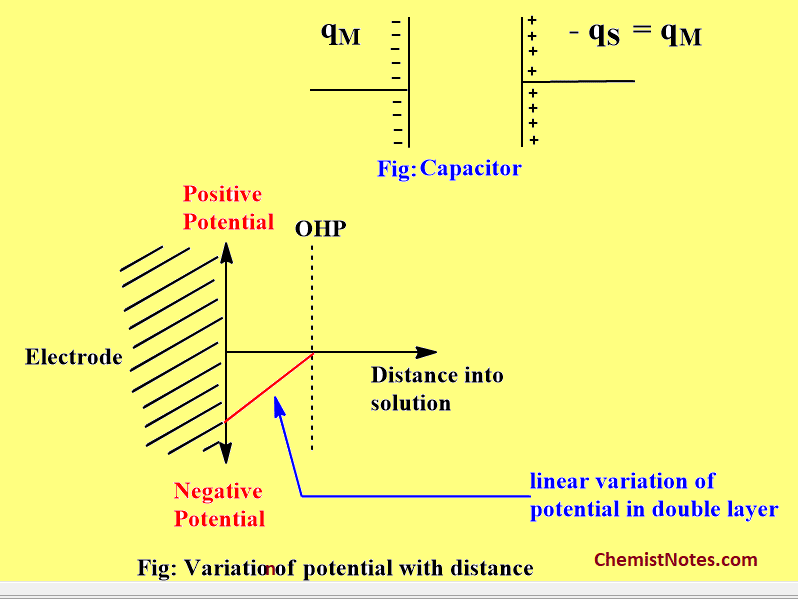
Helmholtz-Perrin model and Electrocapillary curve

The potential difference V across a condenser of a unit area can be given by the following expression.

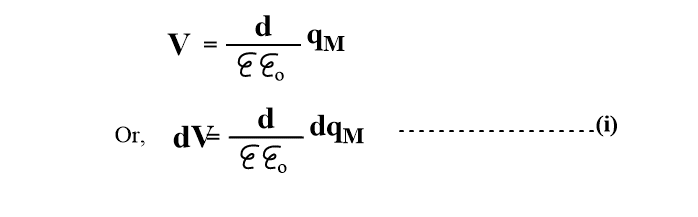
Where, d= distance between plates, ε= dielectric constant of the material between the plates, ε_o=a constant called the permittivity of free space.

From the Lippmann equation,

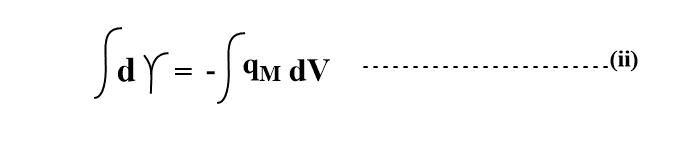
Using the value of dV in equation (ii)

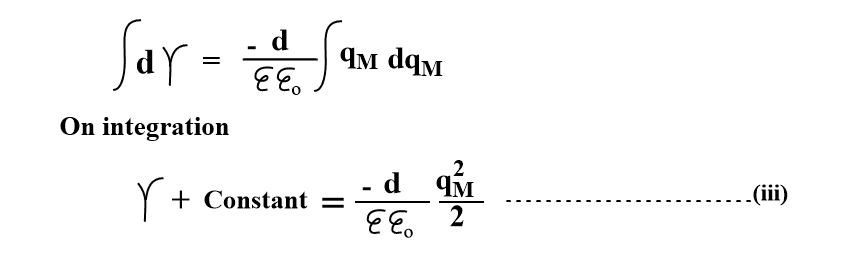
At Point of Zero Charge(PZC), q_M=0 and γ=γ_max .

So, constant= – γ_max

Using these value in equation(iii), we get,

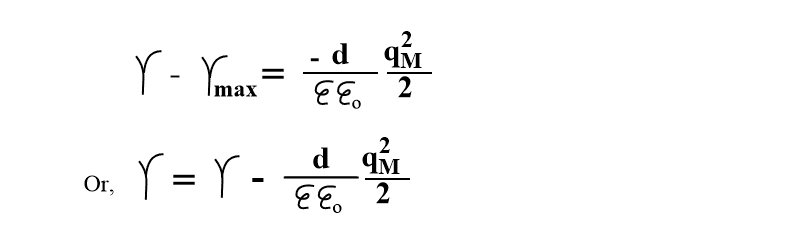
Using the value of q_M from equation(i)

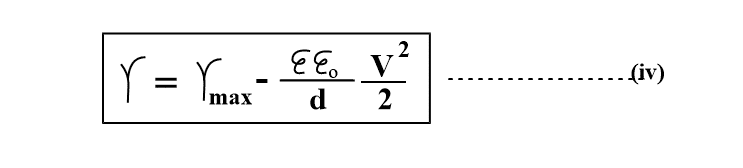
This is the equation for a parabola symmetric about γ_max or electrocapillary maxima(ecm). Therefore, the HP model would be quite satisfactory for a perfect parabola electrocapillary curve.

Failure of Helmholtz-Perrin model

The major limitations of the Helmholtz-Perrin model have been listed below.

1. This model can not explain the experimental electrocapillary curve having a slight asymmetry.
2. This theory fails to explain the dependence of capacity on potential.
3. This model can not explain the variation of differential capacitance with dielectric constant.
4. The effect of nature and types of ions are not considered in this model.

Reasons for failure of Helmholtz-Perrin model

1. A fundamental problem is assigning a value for the dielectric constant of the solvent in the thin Helmholtz region.
2. Solvent structures in the interfacial region differ considerably from that of the bulk solution.
3. The dielectric constant may also vary rapidly with distance in the interfacial region.
4. There are some considerable dielectric saturation effects, so the value of the dielectric constant will be much lower than that associated with the bulk solution.

Helmholtz double layer video