Table of Contents
TogglePauli Exclusion principle was proposed by an Austrian scientist, Wolfgang Pauli who studied atomic spectra of elements in 1945. Pauli was awarded Nobel Prize in Physics in 1925 for his significant contribution through the discovery of a new natural rule, the exclusion principle, or Pauli’s principle. According to this principle, “no two electrons in an atom can have the same set of all four quantum numbers.”
Pauli Exclusion Principle definition
Pauli’s Exclusion principle states that no two electrons in an atom or molecule can have the same quantum numbers. Because of the fact that an orbital can only hold two electrons at a time, the two electrons must have opposing spins. This indicates that if one electron is allocated to spin up (+1/2), the second electron must be assigned to spin down (-1/2).
Pauli Exclusion principle Example
As an illustration of Pauli’s Exclusion Principle, consider neutral helium (He) atom. As shown in the figure below, the helium (He) atom has two electrons in its 1s orbital. Thus, by the principle of quantum numbers and the Pauli exclusion principle, the quantum numbers of these two electrons of the He atom are:

The ‘+’, and ‘-‘ sign in spin quantum number signifies the clockwise and anticlockwise spin of the electron. As explained above, electrons of the He atom having the same value of three quantum numbers (n, l, m), have different values of spin quantum number (s). Thus, the two electrons have a different set of quantum numbers and therefore signify the validity of this principle.
This also made an observation that an orbital can only contain a maximum of two electrons with opposite spin.
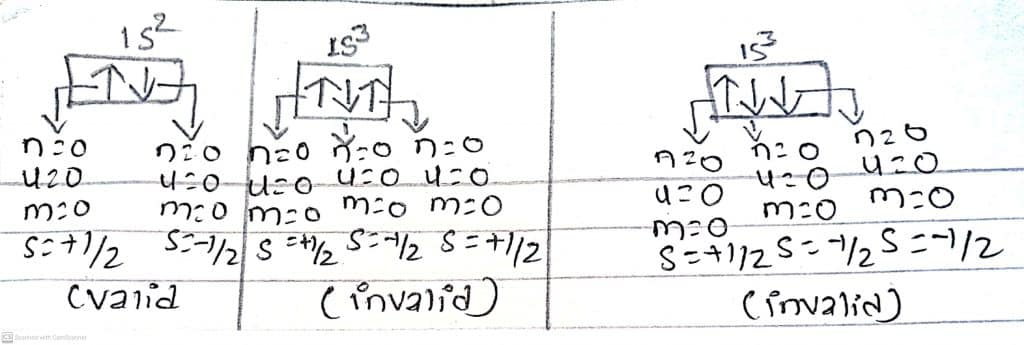
As shown in the figure, two sets of quantum numbers (n, l, m, s) are the same for the 1s3 electronic configuration, while the two electrons present in 1s2 have different sets of quantum numbers. This is the reason 1s3 configuration doesn’t exist,] proving that an orbital can only contain a maximum of 2 electrons.
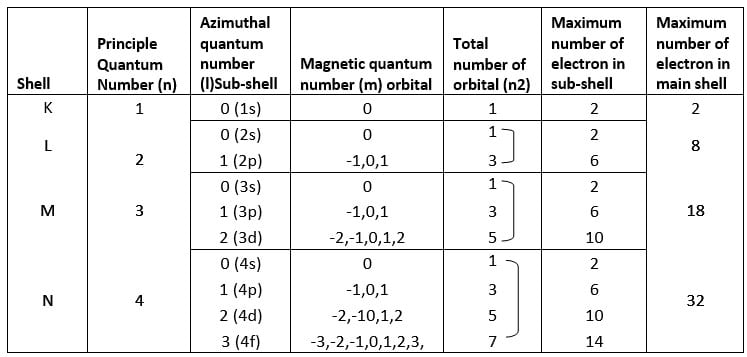
Thus, the maximum number of electrons that can be accommodated in a shell, sub-shell, and orbitals can be predicted by this principle.
Pauli Exclusion principle violation
Let us consider the Berrylium atom (Be). Be has a total of 2 electrons in its 2s orbital. According to the principle of quantum numbers, Hund’s rule, and Pauli Exclusion principle,

In the first case, both the electrons have different values of spin quantum numbers; +1/2 for an upward spin and -1/2 for a downward spin, while the rest of the 2 cases explained in the figure have the same set of all four quantum numbers, and hence violates Pauli’s exclusion principle. Therefore, the first case is valid which explains that two electrons in an orbital must have different sets of quantum numbers.
Hund’s rule and Pauli Exclusion Principle
Hund’s rule refers to a set of rules that are used as the guidelines for filling electrons in the orbital and the spin of an electron in the orbital. Hund’s rule states that” In the orbitals of the same subshell, electrons are filled singly first before pairing starts.
According to the Pauli’s Exclusion Principle, “no two electrons in an atom can have the same set of all four quantum numbers.”
Aufbau and Pauli Exclusion Principle
| Aufbau Principle | Pauli’s Exclusion Principle |
| According to this Principle, electrons are filled in an orbital in the increasing order of orbital energy level i.e. orbital with lower energy is filled first. | According to this Principle, “no two electrons in an atom can have the same set of all four quantum numbers.” |
Application of Pauli’s Exclusion principle
This principle is very useful to calculate the maximum number of electrons in an orbital. The number of main shells and sub-shell can be calculated with the help of this principle. The table above signifies the application of this principle.
Pauli’s Exclusion Principle Video
FAQs
The Pauli Exclusion principle states that
This principle states that no two electrons in an atom or molecule can have the same set of all four quantum numbers.