Lambert’s law is an empirical relationship that relates the amounts of light absorbed and the thickness of the homogeneous absorbing medium. This law was given by Lambert in 1758.
Lambert’s law definition
According to Lambert’s law, “When a beam of monochromatic light is passed through a solution of a homogeneous absorbing medium, the rate of decrease of the intensity of radiation with the thickness of the absorbing medium is directly proportional to the intensity of the incident radiation.”
The amount of light absorbed by a pure substance follows Lambert law which can be stated alternately as ” equal fractions of the incident radiation are absorbed by successive layers of equal thickness of the light-absorbing substances.” The former statement is mostly used and popular.
Lambert’s law derivation
Mathematically, Lambert’s law can be expressed as,
–dI/db ∝ I
-dI/db=KI ………………………………………….(i)
where I=Intensitiy of light at any thickness b.
-dI/db= rate of decrease of intensity of light with respect to the thickness of the homogeneous medium.
K= a constant called absorption coefficient whose value depends on the nature of the absorbing medium.
On rearrangement of equation (i), we get,
-dI/I=Kdb
If Io is the intensity of incident radiation when b=0, then the intensity of radiation It after passing through any finite thickness b of the medium can be obtained by integrating the above equation.

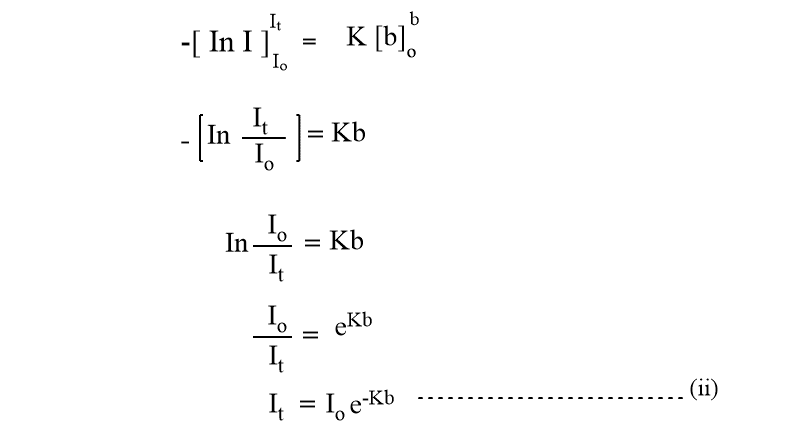
From this equation, it is clear that the intensity of a monochromatic beam of light decreases exponentially when the thickness of the medium increases. Changing natural logarithm to the base 10, equation (ii) becomes,
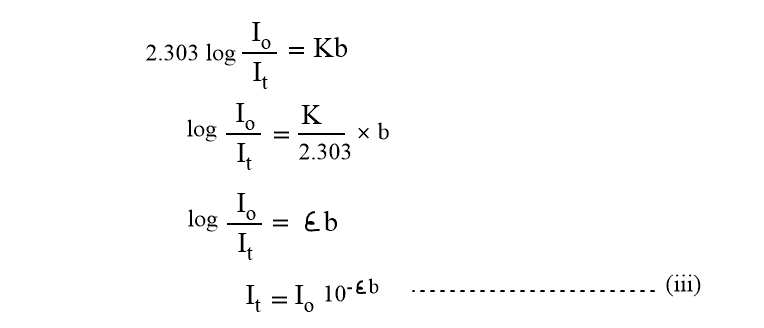
Where, ε = K/2.303, is known as the extinction coefficient of the absorbing medium. Its SI unit is m-1 . Equations (ii) and (iii) are the mathematical expression of Lambert’s law. When ln(Io/ It) is plotted against b, a straight line passing through origin is obtained, having a slope equal to K.