Table of Contents
ToggleDebye Huckel limiting law should be discussed after knowing the concept of ionic strength and activity coefficient of electrolytes. Let’s have some concepts.
What is ionic strength?
Ionic strength can be defined as the total concentration of ions present in the solution. In another word, ionic strength measures the concentration of ionic atmosphere in a solution. It is a dimensionless quantity, it has no unit. It is denoted by μ.
According to the oxford dictionary, ionic strength is a quantity that represents the strength of the electric field in the solution. Ionic strength can be calculated by using the following mathematical expression.
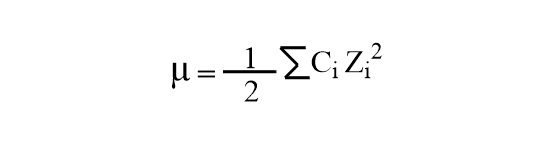
Where, Ci= concentration of ions in MolL-1
Zi= valency of ions
You may have a question about how to do the calculation, right? Ok, let’s have an example.
Calculation of ionic strength of 0.5 M of Cr2(SO4)3 solution.
The ionization of Cr2(SO4)3 takes place as:
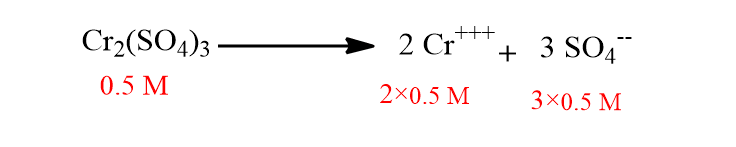
Now, μ= (C1Z12 + C2Z22 )/2
= (1×32 + 1.5×22 )/2
=7.5
Exercise for you: Calculate the ionic strength of 0.2 M solution of FeCl3.
Calculate the ionic strength of 0.1 M KCl and 0.1 M CaCl2 solution.
What is Activity and Activity coefficient ?
The activity of solution can be defined as the effective concentration of an ion or electrolytes. It is denoted by the symbol a. Mathematically, it is defined as,
a= c. f ………………………….(i)
Where c= concentration of the solution in molarity
f= activity coefficient.
For a very dilute solution, the activity of the coefficient is nearly equal to 1 or f=1. So, the activity of the solution becomes equal to the actual concentration of the solution.
On rearranging equation (i), f=a/c
Thus, the activity coefficient is defined as the ratio of activity to the actual concentration of the solution. The activity electrolyte is defined as the product of the activities of cation and anion.
a= a+× a– ……………..(ii)
where a+= activity of cation
a_ = activity of anion.
Similarly, the activity coefficient of electrolytes can be calculated as:
f=f+×f_ ……………(iii)
where f+= activity coefficient of cation
f_ = activity coefficient of the anion.
The activity and activity coefficient can not be determined experimentally but their mean value can be measured. The mean activity of the electrolyte AxBy can be determined by the following relation.
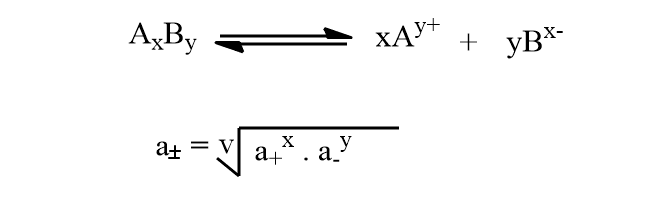
Debye huckel limiting law equation
Debye Huckel limiting law relates the mean activity coefficient of an electrolyte with the valency of ions and ionic strength of the solution. It is applicable only for a dilute solution, so it is called the limiting law.
The debye huckel limiting law equation can be expressed mathematically as:
log10 f± = – A Z+Z– µ 1/2
where f±=mean activity coefficient when concentration is expressed in molarity.
Z+= Valency of cation
Z–= Valency of anion
μ= ionic strength of a solution
A= constant which depends upon a particular solvent at a particular temperature.
When -log10 f± is plotted against µ 1/2, a straight line passing through the origin and having a slope equal to A Z+Z– is obtained.
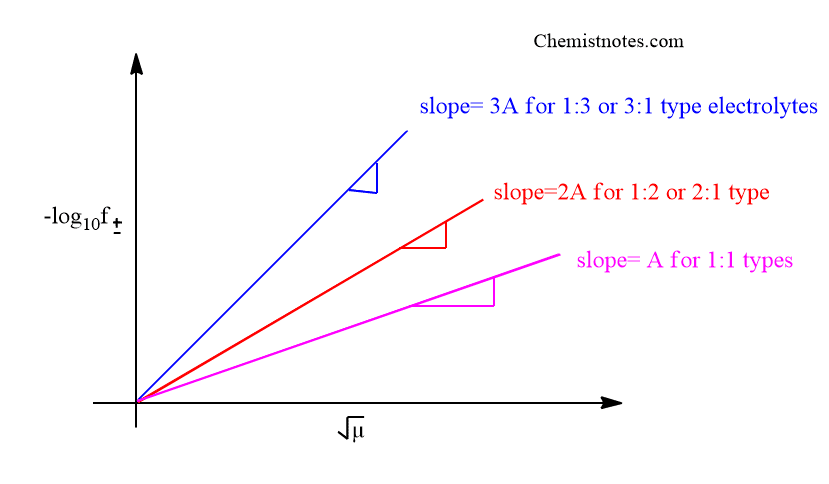
Application of debye huckel limiting law
Debye Huckel limiting law can be used to calculate the mean activity coefficient of an electrolytic solution if the concentration or ionic strength of the solution and the value of A is provided.