Ostwald’s dilution law and its limitations

Ostwald’s dilution law and its limitations are based on the Arrhenius theory of dissociation. According to Arrhenius theory, an electrolyte undergoes dissociation in an aqueous solution and splits into cations and anions. These ions are in equilibrium with each other which is termed ionic equilibrium. It means ions are rapidly dissociating and associating at the same rate.

Ostwald’s dilution law and its limitations

what is ostwald’s dilution law?

Since ions are in equilibrium, Ostwald applied the law of mass action in ionic equilibrium similar to chemical equilibrium. He derived an expression relating to the variation of the degree of ionization of an electrolyte with dilution, such expression is called Ostwald’s dilution law.

The expression of Ostwald’s dilution law can be derived by considering a binary electrolyte AB. Let this electrolyte AB dissociates in water as shown below:

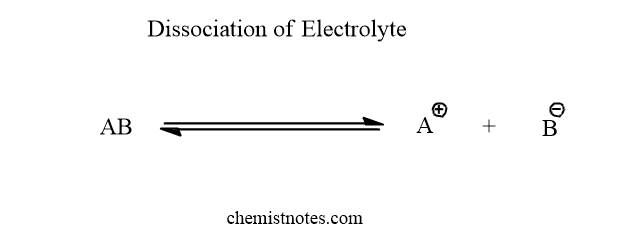
Let C mole/L be the concentration of the electrolytes AB and α be its degree of dissociation. The dissociated ions are in equilibrium and hence, the equilibrium concentration of AB, A^+, and B^– is C(1-α), Cα, and Cα mole/L respectively.

Now, applying the law of mass action to the above ionic equilibrium,

Rate of dissociation=k₁[AB]= k₁× C(1-α)

Rate of association=k₂[A⁺][B^–]= k₂×Cα ×Cα

Since the rate of dissociation and rate of association of electrolytes is exactly equal at equilibrium, we can write,

k₁× C(1-α)=k₂×Cα ×Cα

k₁/k₂= C²α²/C(1-α)

K_c= Cα²/(1-α) …………………………(i)

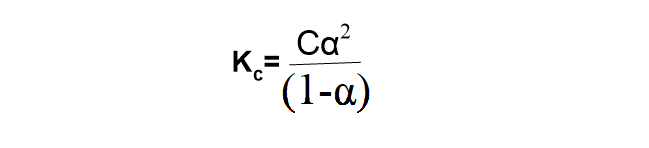
Where K_c= k₁/k₂=equilibrium constant known as ionization constant or dissociation constant, which depends on temperature.

If one mole of electrolyte be dissolved in V liter of the solution then above we can write,

C= n/ V= 1/ V

Using this value in equation (i), the above expression becomes,

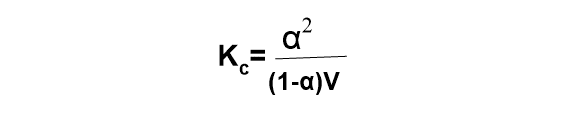
This expression relates to the degree of dissociation of electrolytes with dilution. This is called Ostwald’s dilution law.

There are two cases:

Case 1: For weak electrolytes, the value of the degree of dissociation α is very very low, therefore,

(1-α)= 1 (almost equal to 1). The expression for weak electrolytes becomes,

K_c= α²/ V.

Case 2: For strong electrolytes, the value of the degree of dissociation α is almost equal to one, because strong electrolytes are completely ionized in water. Therefore, the value (1-α) can not be neglected. The above equation remains the same.

K_c= Cα²/(1-α)

Limitations of Ostwald’s dilution law

Ostwald’s dilution law is valid only for weak electrolytes and it completely fails when applied to strong electrolytes. This is because strong electrolytes are completely ionized in solution, the value of the
dissociation constant K decreases with dilution instead of remaining constant.

The factors responsible for the failure of Ostwald’s dilution law are listed below:

1. Ostwald’s dilution law is based on Arrhenius theory. According to which, only a fraction of electrolytes are dissociated at normal dilution but completely dissociated in infinite dilulation. This is valid for weak electrolytes. But strong electrolytes are almost compeletly dissociated at all dilution, therefore does not give accurate value of degree of dissociation.
2. Ostwald’s dilution law has applied law of mass action. When the concentration is very high, the equilibrium is affected by presence of charges. Therefore, simple form of law of mass action can not be applied in such case.
3. The dissociated ions may get hydrated by water molecules (solvated), which may alter the concentration of ions.

References

1. Arun Bahl, B. S. Bahl & G. D. Tuli, Essentials of Physical Chemistry, S. Chand and CompanyLtd., New Delhi, 2012
2. M. L. Sharma & P. N. Chaudhary, A Textbook of B. Sc. Chemistry (Volume II), 2nd Edition, Ekta Books Nepal, 2007