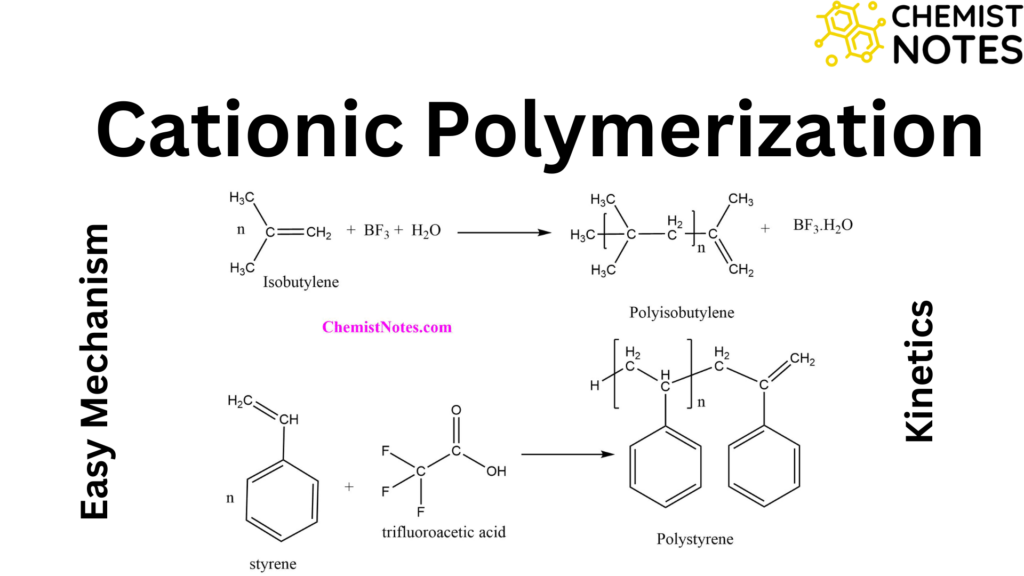
Unimolecular reactions are considered to be one of the simplest concepts in terms of reactions in chemistry. Unimolecular reactions are especially fascinating because their rate constants vary with pressure. The pressure dependence results from collisional energy transfer, which is required for the activation and deactivation of vibrationally excited reactants.
Lindemann’s theory
Lindemann tried to explain the mechanism of unimolecular reaction on the basis of bimolecular collision. According to this theory, the activated molecules that have formed due to bimolecular collision do not convert immediately into the product. There exists a certain time lag between the activation and the reaction. Because of this time lag, the activated molecules may be deactivated by collision with another molecule. So, the rate of reaction does not depend on all the molecules that are activated but only on those that remain active for a long time and are converted into a product.
Let us consider a general reaction:

Since A* is an activated complex and acts as an intermediate. So, the steady state approximation principle can be applied to them. So, according to the steady-state approximation principle,
Rate of formation A* = Rate of consumption of A* i.e.
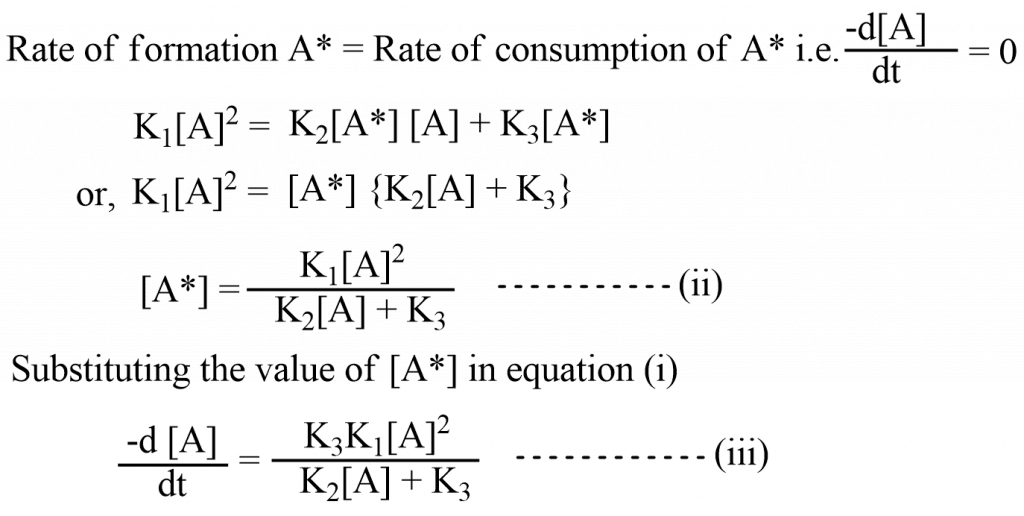
Case I. When K2 [A] >>> K3, then K3, then K3 can be neglected in the denominator of equation (iii) so, equation (iii) becomes.

This implies that the reaction will be of 1st order. This condition appears only when the concentration of normal molecules is high as compared to the activated molecules and hence the rate of deactivation becomes high as compared to the rate of activation.
Case II. When K 3 >>> K2 [A], then K2 [A] can be neglected in the denomination of equation (iii), So equation (iii) becomes:
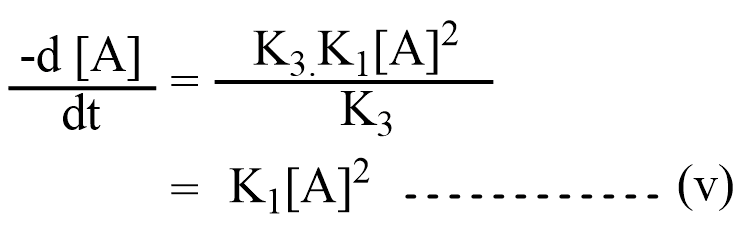
This is simple in that the reaction follows 2nd order. This condition appears only when the rate of activation is higher as compared to the rate of deactivation.