Table of Contents
ToggleMass defect is the difference between the theoretical mass and the actual mass (experimental mass) of an atom. It is denoted by Δm. Binding energy is the energy that is released in the formation of a nucleus from its constituent nucleons (protons + neutrons). A detailed explanation of the mass defect and binding energy is presented below:
Mass Defect
It is well known that an atom consists of protons and neutrons, which together constitute nucleons. Thus, it is expected that the mass of an atomic nucleus will be equal to equal to the sum of the masses of these nucleons. However, it has been found that the actual mass of a nucleus is always less than the sum of masses of neutrons and protons. This difference between the experimental and calculated mass of the nucleus is called mass deffect.
The mass defect formula is:
Mass defect (Δm) = Theoretical mass – Actual mass (Experimental)
= (mass of protons + mass of neutrons) – Actual mass
Let us consider 42He molecule consisting of two protons and two neutrons.
Mass of neutrons = 2 ×1.00898 = 2.01796 amu
Mass of protons = 2 ×1.00813 = 2.01626 amu
Total masses (Theoretical) = 4.03422 amu
Mass of 42He (Experimental) = 4.00387 amu
∴ Mass defect (Δm) = (4.03422 – 4.00387) amu = 0.03035 amu
The theoretical explanation of mass defect is based on Einstein’s equation, E = mc2. When a certain number of protons and neutrons combine to make a nucleus, some of the mass (Δ) disappears because it is converted into energy. This energy is called binding energy which is the amount of energy released when protons and neutrons combine to form the nucleus.
Binding energy
The energy released in the formation of a nucleus from its constituent’s nucleons is called the binding energy of the nucleus. This much energy is to be supplied to break up the nucleus into its constituent particles.
The energy equivalent to mass defect i.e. Binding energy can be illustrated as:
Protons + Neutrons → Nucleus + Binding energy
Nucleus + Binding energy → Protons + Neutrons
If Δm is the mass defect in amu, then the binding energy = Δm × 931 MeV (1 amu = 931 MeV)
Thus, the higher the mass defect, the greater will be the binding energy. The binding energy of the nucleus increase with the increase in the number of nucleons in the nucleus. Binding energy of a nucleus is a measure of nuclear stability. The magnitude of the binding energy of a nucleus determines its stability against disintegration, if the binding energy is large the nucleus is stable i.e. the greater the binding energy per nucleon, the more stable is the nucleus.

The nuclear binding energy increases with the atomic number of the element. This suggests that heavier nuclei have greater energy than lighter ones. Because of this, heavier nuclei ought to be more stable. However, the heavier nuclei, which are radioactive elements that occur naturally, are known to be unstable.
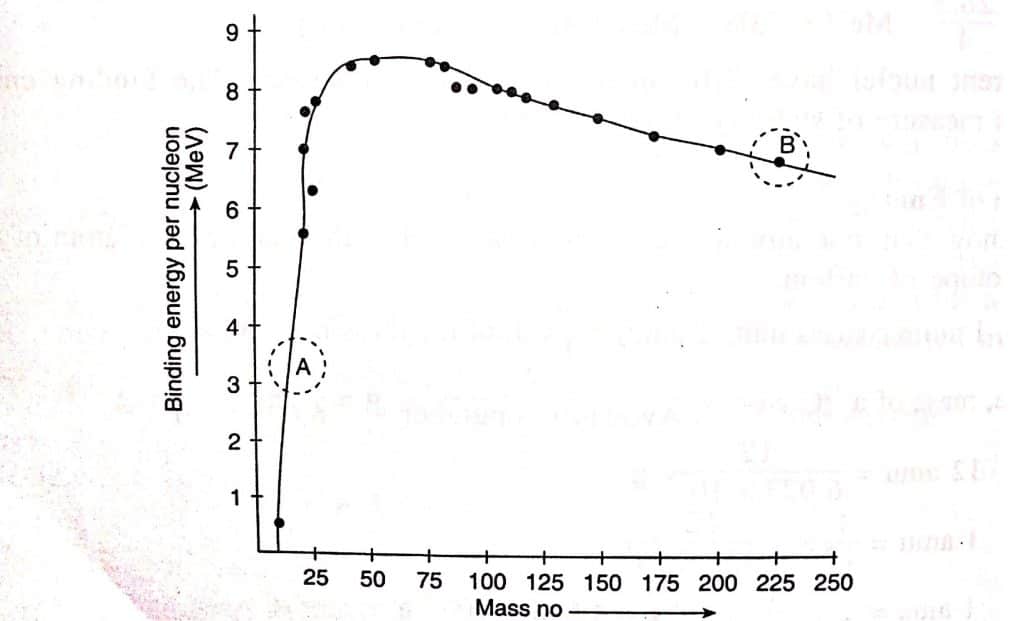
The maximum in the curve corresponds to the nucleus with the highest binding energy per nucleon and hence corresponds to the maximum stability. The heavier element possesses very low binding energy per nucleon, and have unstable nuclei. Because of this, lighter nuclei tend to unite to produce stable intermediate atomic mass nuclei, whereas heavy nuclei tend to disintegrate into those of intermediate atomic mass.
Mass defect and Binding energy video
FAQs
Binding energy of nucleus is
Binding energy of nucleus is the energy released when nucleons come together to form the nucleus from infinite separation.
binding energy formula
binding energy = Δm × 931 MeV, where Δm is the mass defect.
define mass defect
The difference between experimental and calculated masses is called the mass defect.
References
- Atkins, P. (2010). Shriver & Atkins’ Inorganic Chemistry (5th or later Edition). Oxford University Press.
- Lee, J. D. (2008). Concise Inorganic Chemistry: Fifth Edition by J.D. Lee (Fifth edition). Oxford University Press.
- Arun Bahl, B. S. Bahl & G. D. Tuli, Essentials of Physical Chemistry, S. Chand and Company Ltd., New Delhi, 2012.