Table of Contents
ToggleIn 1905, Albert Einstein proposed that light can behave both as a wave and as a particle, implying that it has a dual character. The French physicist Louis de Broglie suggested (1924) a hypothesis to explain the theory of atomic structure, and is therefore the hypothesis is also referred to as the de Broglie hypothesis. The de Broglie hypothesis states that any moving particle/object is associated with both the wave properties as well as particle properties. Later on, Davisson and Germer proved the hypothesis experimentally while studying the diffraction of electrons.
de Broglie Equation Definition
According to de Broglie equation/hypothesis, “a matter particle in motion is also associated with waves.” In other words, any moving microscopic or macroscopic particle will be associated with a wave character. Such waves are also called matter waves or de Broglie waves. de Broglie equation is basically used to define the wave properties of matter/electron. Thus, the matter particle-like electrons show dual character i.e. it behaves like a particle as well as a wave.
According to de-Broglie, the particle with wavelength and mass ‘m’ moving with velocity ‘v’ is represented by the relation:
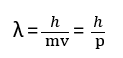
de Broglie wave equation derivation

de Broglie equation significance
The de-Broglie equation is significant only for sub-microscopic objects in the range of atoms, molecules, or smaller sub-atomic particles. The wave nature of matter, on the other hand, has no meaning for ordinary-sized objects because the wavelength of the wave associated with them is too small to detect.
de Broglie Hypothesis video
FAQs/MCQs
What is h in de broglie equation?
h in de Broglie equation is Planck’s constant having a value of 6.62607 x 10-34 J s
What is the significance of de Broglie equation?
The de-Broglie equation is significant only for sub-microscopic particles that are in the range of atoms, molecules, or smaller sub-atomic particles.
Derive de Broglie equation for microscopic particle.
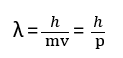
According to de Broglie equation/hypothesis, “a matter particle in motion is also associated with waves.”