Table of Contents
ToggleDebye huckel Onsager equation is a mathematical expression that relates the variation of equivalent conductance with the concentration of electrolyte solutions.
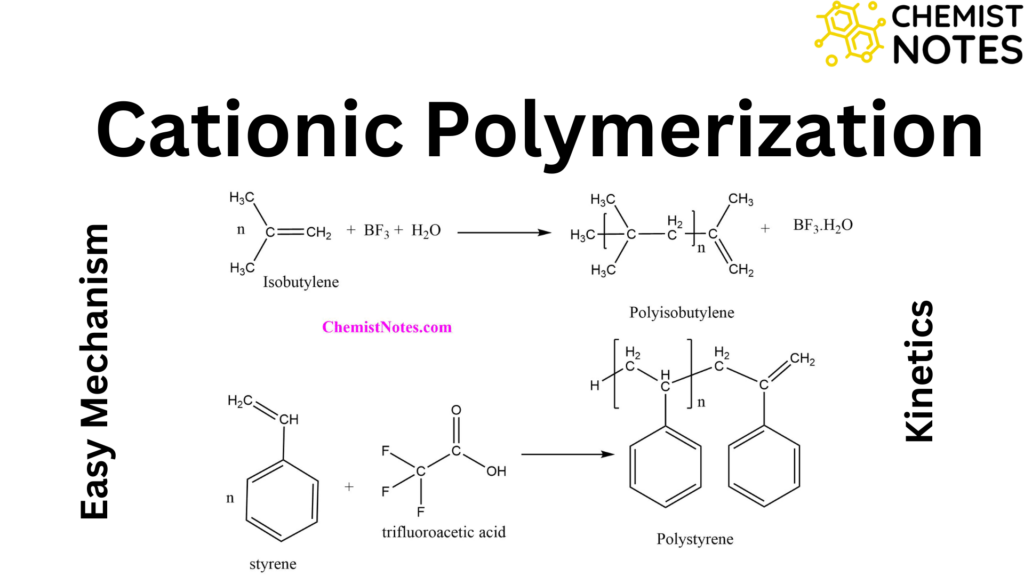
Debye huckel onsager equation
Debye and Huckel initially derived an equation to describe how the equivalent conductance of electrolytic solution changes on dilution. Later this equation was further improved by Onsager and now this equation is known as Debye huckel Onsager equation.
Mathematically, Debye huckel Onsager equation can be expressed as,
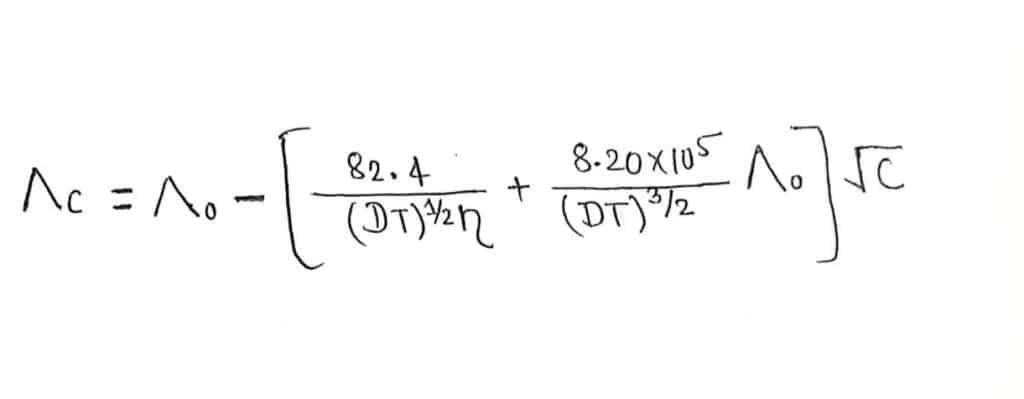
Where, Λc= equivalent conductance at a given concentration
Λo= equivalent conductance at infinite dilution
D= Dielectric constant for the medium or solvent
η= Viscocity of the solvent
T= Absolute temperature
C= concentration
For a particular solvent at a particular temperature, the debye huckel Onsager equation can be written as
Λc=Λo-(A+BΛo ) C1/2 ……………………………………(ii)
Where A and B are constant at a given temperature, Whose values can be calculated as
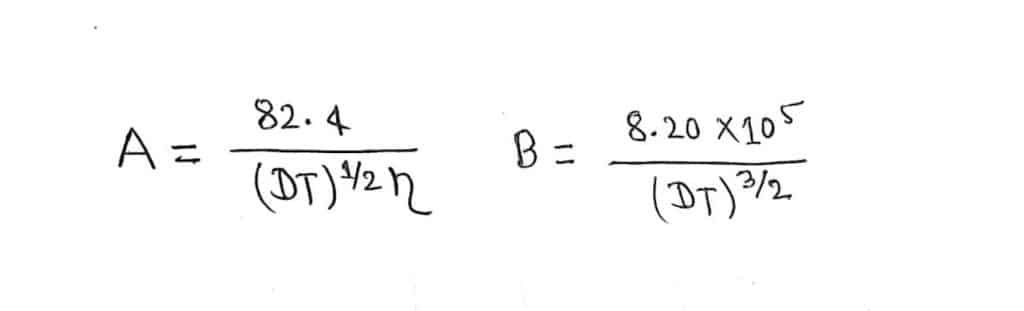
If water is solvent and at a temperature of 25°C, the value of A is taken as 60.20, and the value of B is taken as 0.229.
Debye huckel onsager equation graph
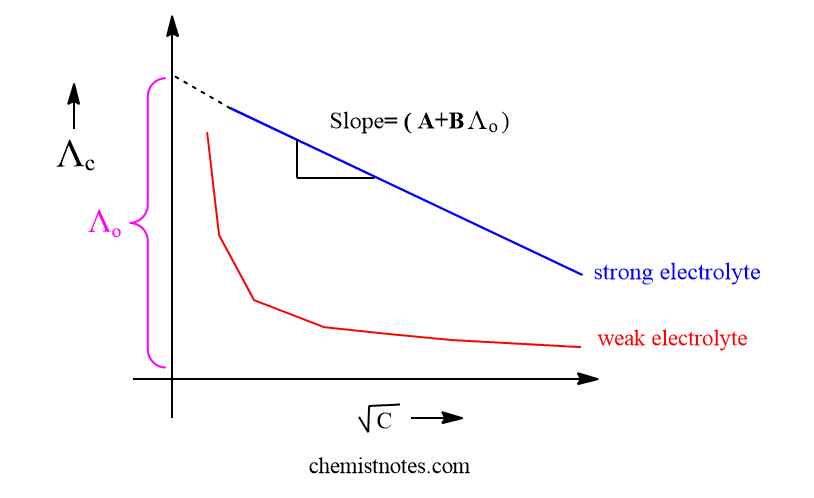
When Λc is plotted against C1/2 ( Under root C), a straight line having a negative slope (A+BΛo) and intercept Λo is obtained. Therefore, from the slope, we can determine the values of equivalent conductance of strong electrolytes at infinite dilution.
Limitations of debye huckel onsager equation
The graph of Λc versus C1/2 shows that the equivalent conductance of weak electrolyte decreases exponentially with concentration so that equivalent conductance at infinite dilution ( Λo) for weak electrolyte can not be determined from the above curve on extrapolation. Therefore, the Onsager equation is limited only for strong electrolytes and invalid for weak electrolytes.