Table of Contents
ToggleAccuracy and precision are the two important terminologies used in any measurement. These two terms describe how closely a measurement resembles a standard or known value. Accuracy defines the degree to which a measurement is close to its true value. However, precision defines how consistently the same results are obtained from repeated measurements under the same circumstances. Measurements can be both precise and accurate, precise but not accurate, accurate but not precise, or neither.
The in-depth discussion on accuracy and precision is illustrated below:
Accuracy
Accuracy indicates the closeness of the measurement to the true or accepted value. It is always expressed by absolute and relative error. This measures the agreement between the result and the accepted value. Accuracy is often more difficult to determine because the true value is really unknown. The accepted value must be used instead of the true value.
The comparison of two types of data is always made on the basis of an inverse measure of accuracy which is an error. The smaller the error measured the greater the accuracy.
The accuracy has been classified into 3 types:
- Point Accuracy: Point accuracy denotes that the instrument’s accuracy is only applicable to that specific point on its scale. This kind of accuracy, however, says nothing about the instrument’s overall accuracy. An excellent illustration of point accuracy is mass measurement.
- Accuracy as Percentage of True Value: When the accuracy of the instrument is evaluated by comparing the measured value to its true value, the result is expressed as a percentage of the true value. Up to 0.5 percent of the true value is ignored due to instrument accuracy.
- Accuracy as Percentage of Scale Range: The accuracy of a measurement is expressed as a percentage of the scale range.
Precision
Precision describes the reproducibility of measurements. In other words, precision can be defined as the closeness of results that have been obtained in exactly the same way. The precision of a measurement can be easily measured by simply repeating the experiment to obtain a replicated sample.
The precision of measurement is generally measured by the standard deviation, variance, and coefficient of variation. These are functions of deviation from the mean. The precision can be also expressed in terms of the range of data. It doesn’t tell anything about true value.
Precision includes two important terms:
- Repeatability: The fluctuation that results from taking multiple measurements under the same circumstances in a short period of time.
- Reproducibility: The variation appears when employing the same measurement technique with various instruments, and operators, and over extended time periods.
The well-precise value may be inaccurate. The accurate value may not be precise sometimes. The determinate type of error which lead to inaccuracy may or may not affect precision depending on how nearly it remains constant throughout that series of experiment. This indicates accuracy and precision of data are not indicative of each other.
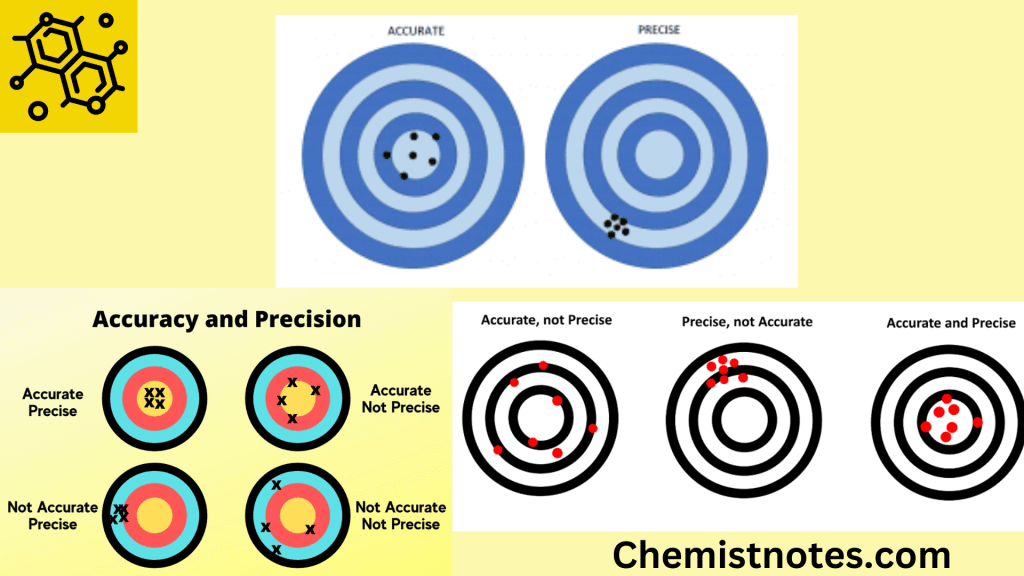
Accuracy and Precision Examples
Imagine a football player aiming at the goal to get a concept of accuracy and precision. The player is considered accurate if his shot finds the net. A football player who repeatedly strikes the same goalpost is precise but not accurate. Therefore, if a football player strikes the ball all over the place but still scores, he or she is accurate without being precise. Whether he/she scores or not, a precise player will consistently strike the ball to the same spot. A precise and accurate football player will not only aim at a specific spot but also score a goal.
Difference between Accuracy and Precision
| Accuracy | Precision |
| Accuracy defines the closeness of the measurement to the true or accepted value | Precision defines the reproducibility of measurements. |
| Measurement can be accurate but not necessarily precise. | Measurement can be precise but not necessarily accurate. |
| Indicates how closely the results match the reference value. | Indicates how closely results agree with one another. |
| Can be calculated using just one measurement. | Requires a number of measurements to be calculated. |
| May be affected by the determinate error. | May be affected by the indeterminate error. |