Table of Contents
ToggleMichaelis-Menten equation
Michaelis-Menten equation is a mathematical equation that relates the rates of enzyme-catalyzed reaction with the concentration of both substrate and enzyme. This equation/model was given derived by two scientists Leonor Michaelis and Maud Leonora Menten in the 20th century to describe the variation of rate of the chemical reaction catalyzed by enzymes.
In order to study enzyme kinetics experimentally, enzyme-catalyzed reactions are carried out by monitoring the initial rate of product formation.
Assumptions of the Michaelis Menten equation
To derive the Michaelis Menten equation, the following principle features of many enzymes catalyzed are considered.
- For a given initial concentration of substrate [S]o, the initial rate of product formation is proportional to the total concentration of enzyme [E]o.
- At low concentrations of substrate [S]o, the rate of product formation varies linearly with substrate concentration i.e rate is proportional to [S]o.
- At a high concentration of substrate, the rate of product formation becomes independent of substrate concentration reaching a maximum value known as the maximum velocity, Vmax.
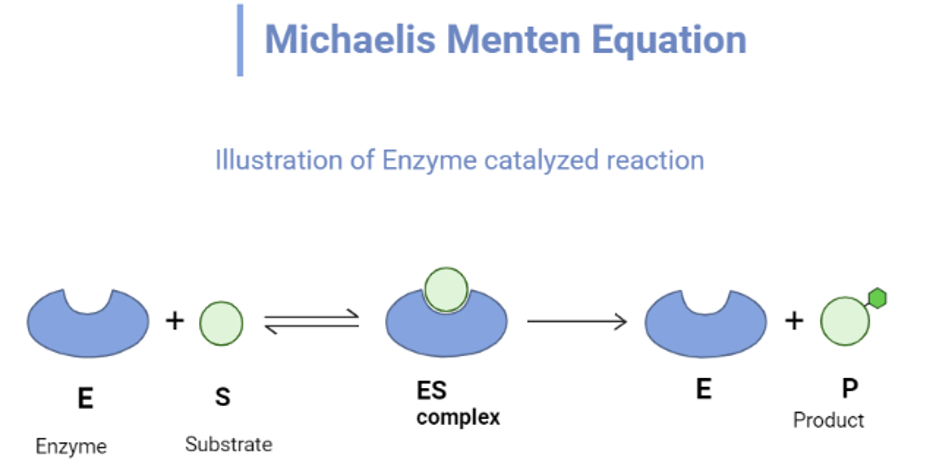
Derivation Michaelis Menten equation
According to Michaelis Menten’s mechanism, an enzyme-substrate complex is formed in the first step and the complex may either dissociate to give substrate or be converted to give a product.
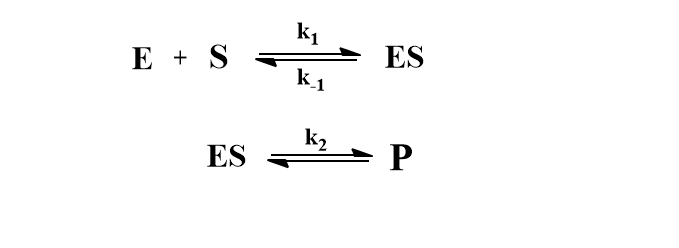
Where E and S are enzyme and substrate respectively, P is the product and ES is complex.
The rate of product formation according to the Michaelis Menten mechanism can be represented as

Applying steady-state approximation to obtain the concentration of enzyme-substrate complex[ES].
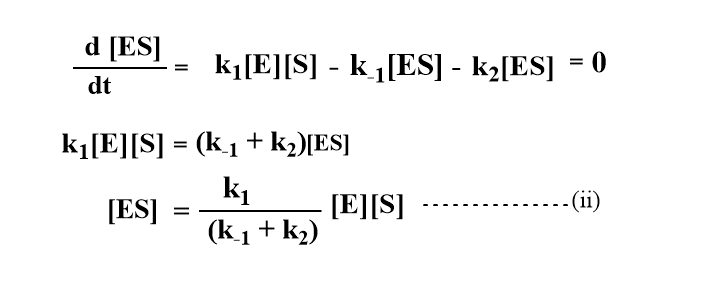
Since the molar concentration of substrate is usually very much greater than that of the enzyme, only a small proportion of substrate is bound to the enzyme. The total concentration of enzyme[E]o is equal to the concentration of free enzyme [E] plus the concentration of the complex.
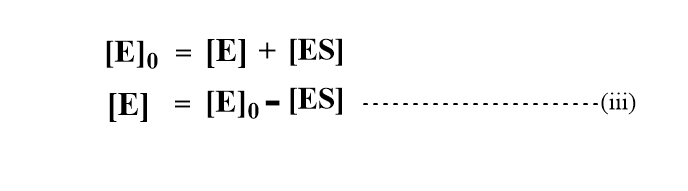
Using the value of [E] in equation (ii).
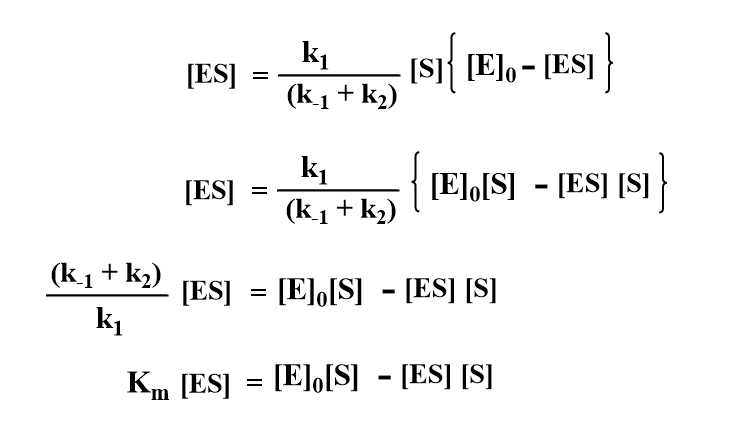
where km=(k-1 + k2)/k1, known as the Michaelis Constant which is the characteristics of a given enzyme acting on a given substrate.
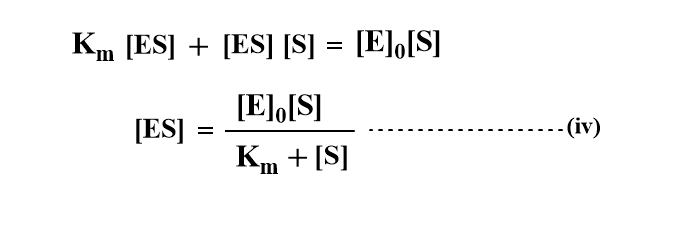
Using the value of [ES] in equation (i)
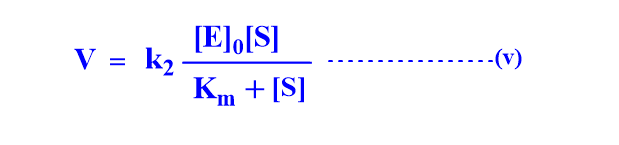
Equation (v) is known as Michaelis- Menten equation.
Case I: When [S] <<<< Km, term [S] can be neglected in the denominator.

Case II: When [S] >>>> Km, the term Km can be neglected.
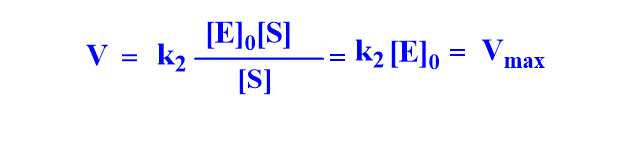
This indicates the kinetics is in zero order. Vmax is the limiting rate at a high substrate concentration, also known as maximal velocity.
Case III: When [S] = Km
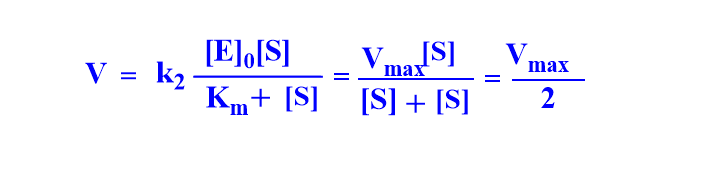
Graphical representation of Michaelis-Menten equation
From the Michaelis-Menten equation,

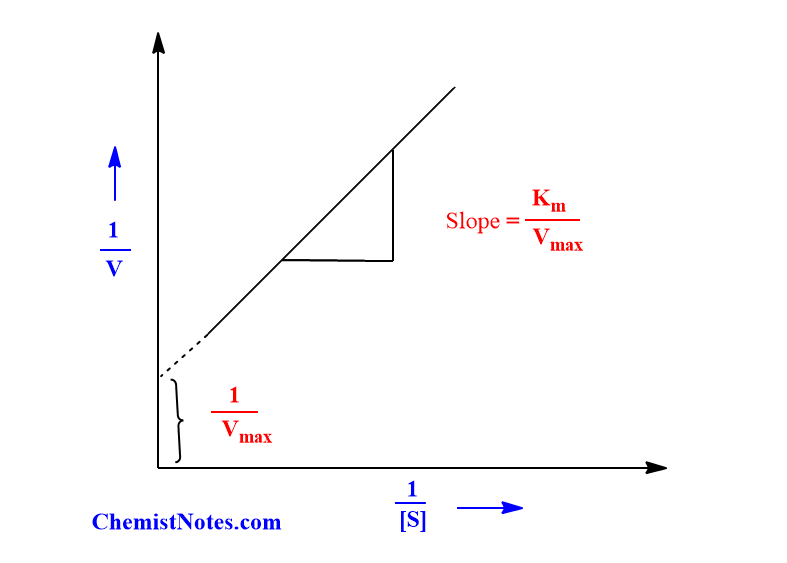
When (1/V) against (1/[S]) is plotted, a straight line is obtained which on extrapolation gives y-intercept at 1/Vmax and slope equal to { km/Vmax}.
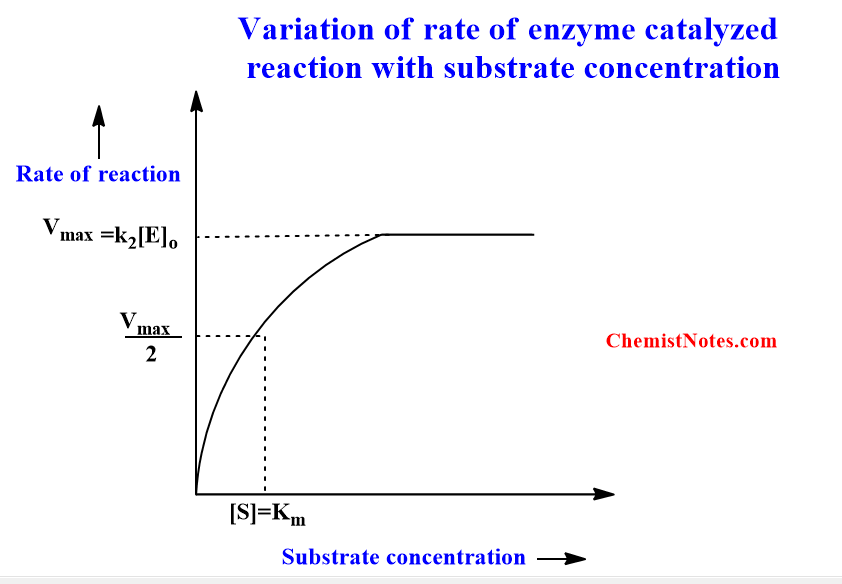
How does the rate of enzyme-catalyzed reaction vary with substrate concentration?
Initially, the rate of an enzyme-catalyzed reaction increases linearly with the substrate concentration but later on increasing the substrate concentration, the rate becomes constant and highest as well, this rate is known as maximum velocity. The following picture depicts the variation of rate with substrate concentration.
Significance of km in Michaelis Menten equation
The Km is Michaelis constant and it can be defined as the substrate concentration at which the rate of reaction is half of the maximum velocity(Vmax). Km represents the affinity of an enzyme for a particular substrate. It means the lower the value of Km, the greater the enzyme’s affinity for the substrate. We can say that the value of Km and the affinity of the enzyme has an inverse relationship.
Significance of Vmax in Michaelis Menten equation
The Vmax represents the maximum limiting velocity obtained when there is a sufficiently higher substrate concentration. At sufficiently higher substrate concentration, all the binding sites of enzymes are already occupied by the substrate so that the rate of reaction achieves a constate value. Therefore we can say that Vmax is the rate of an enzyme-catalyzed reaction achieved when the binding sites of the enzyme are fully saturated by the substrate.
Limitations of Michaelis Menten equation
- This equation does not take into consideration the impact of enzyme inhibitors or activators on the rate of reaction.
- The allosteric regulation that has a significant impact on enzyme kinetics is not considered by this equation.
- This equation makes the assumption that the reaction is occurring at the constant temperature and pH, thus does not take into consideration variations in these parameters that can have an impact on the reaction rate.