Table of Contents
ToggleThe difference between the freezing point of the pure and the solution containing the involatile solute is called the depression of freezing point. The freezing point is a point where the chemical potential of its liquid and solid phases is equal. It is colligative property because it depends only on the amount of the solute added to a given solvent. If To is the freezing point of a pure solvent, Tf is the freezing point of the solution, then the freezing point of depression Tf is given by:
To – Tf = ΔTf
Depression of Freezing Point Graph
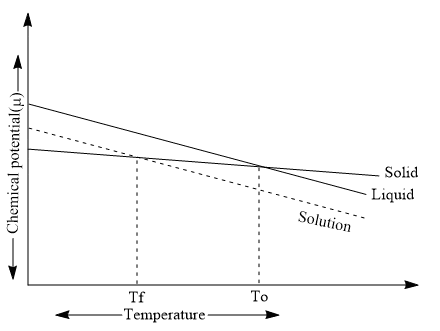
Let us consider the freezing of a pure liquid solvent. As its freezing point equilibrium exists between solid and liquid, and the escaping tendencies in the two phases are identical, i.e., the vapor pressure of the solid phase and liquid phase are similar in their chemical potentials. But, as the involatile solute is added to the liquid phase, the proportion of molecules bouncing against the solid phase decreases. The escaping tendency of solvent molecules from liquid to solid has been diminished, whereas the reverse escaping tendency (solid to liquid) is unaffected and crystals of solvent begin to dissolve. To prevent this and restore equilibrium, we must favor the solid phase by lowering the temperature. At some lower temperature, the two escaping tendencies again match, and equilibrium is attained.
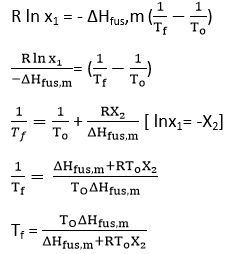
Thus, this implies that on the addition of solute to the solution, the freezing point can be lowered.
Molal Freezing Point Depression
Tf = Kf m
Where,
ΔTf is freezing point depression and the proportionality constant Kf, is called the molal freezing-point depression constant. It is a constant that is equal to the change in the freezing point of a 1 molal solution of a non-volatile molecular solute dissolved per kg of solvent. For water, the value of Kf is -1.86°C/m. So the freezing temperature of a 1-molal aqueous solution of any nonvolatile molecular solute is -1.86 °C. Every solvent has a unique molal freezing-point depression constant.
Its value can be evaluated experimentally,
we have,

Molal freezing point depression constant for some solvents:
| Solvent | Normal freezing point (oC) | Molal freezing-point depression constant Kf (oC/m) |
| Acetic acid | 16.6 | -3.90 |
| Camphor | 178.8 | -39.7 |
| Naphthalene | 80.2 | -6.94 |
| Phenol | 40.9 | -7.40 |
| Water | 0.00 | -1.86 |
Determination of Molecular weight of solute from Depression of Freezing point
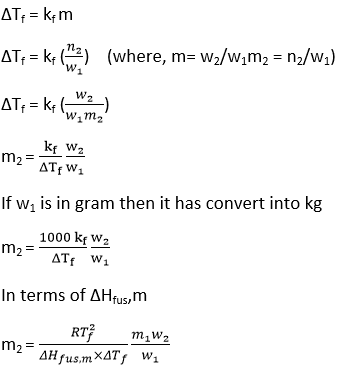
Numerical problem
Calculate the molal freezing point depression constant for benzene
If its heat of fusion at 5oc is 9.83 kJmol-1.
Solution: Given, To = 5 + 273.15 = 278.15k , m1=78 g mol-1
ΔHfus= 9830Jmol-1
R=8.314 J mol-1 k-1
Kf = ?
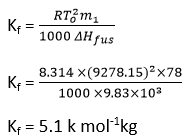
Freezing point of some of the Compounds
| Compound | Freezing Point (oC) |
| Acetic acid | 16.6 |
| Benzene | 5.5 |
| Camphor | 179.8 |
| Carbon disulfide | -112 |
| Carbon tetrachloride | -23 |
| Chloroform | -63.5 |
| Cyclohexane | 6.4 |
| Ethanol | -114.6 |
| Ethyl ether | -116.2 |
| Naphthalene | 80.2 |
| Phenol | 41 |
| Water | 0 |
Application of Depression of Freezing point
The freezing-point depression prevents radiators from freezing in winter. Road salting takes advantage of this effect to lower the freezing point of the ice it is placed on. Lowering the freezing point allows the street ice to melt at lower temperatures, preventing the accumulation of dangerous, slippery ice. Some creatures that live in extreme cold use depression of freezing point. Such species have evolved means for producing high concentrations of sorbitol and glycerol, among other substances. The freezing point of the water inside them is lowered by the increased solute concentration, keeping the organism from freezing solid even when the water around them freezes or the air around them becomes extremely cold.
Depression of freezing point Video
FAQs
What is the depression of freezing point?
The difference between the freezing point of the pure and the solution containing the involatile solute is called the depression of the freezing point.