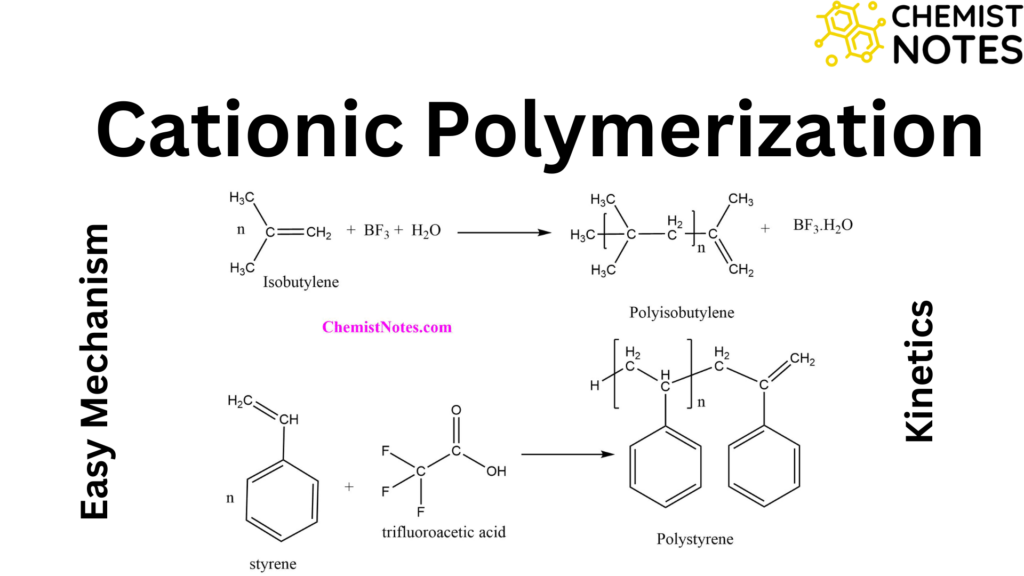
Table of Contents
ToggleIn 1913, W.L Bragg and his father W.H. Bragg used X-rays to determine the mathematical equation called Bragg’s equation so as to calculate interatomic distances from X-ray diffraction patterns. According to Bragg’s law, “When an x-ray strikes a crystal surface, its angle of incidence, θ, reflects back with the same angle of scattering, θ, and leads to constructive interference when the path difference, d, is equal to a whole number, n, of wavelengths”. The relationship between an x-ray light incident onto a crystal surface and its reflection from it is well explained by this law.
Bragg’s equation states that:
- The principles of reflection govern the X-ray diffracted by atoms in crystal planes.
- If the excess distance traveled by the second ray is an integral number of wavelengths, the two rays reflected by subsequent planes will be in phase.
Bragg’s equation for X-ray diffraction
When two beams of the light of the same wavelength come from two different sources and meet at a point they can reinforce or cancel each other. If the waves are in phase and reinforce each other, a bright light appears. This phenomenon is called constructive interference. If the waves are partially or completely out of phase, no light or very dim light is observed. This is called destructive interference. In 1912, Max Van Laue observed found that the same behavior is observed when the X-rays are diffracted from a crystal (copper sulphate).
A monochromatic X-ray beam is incident at a single crystal through slits. The diffracted beams are captured on a photographic film. The diffraction patterns are analyzed to determine the inter-planar distance. Bragg studies the phenomenon of diffraction of X-rays by crystal and derived a simple relation between the distance between the layers and wavelength of X-rays used and the angle of diffraction called the Bragg equation.
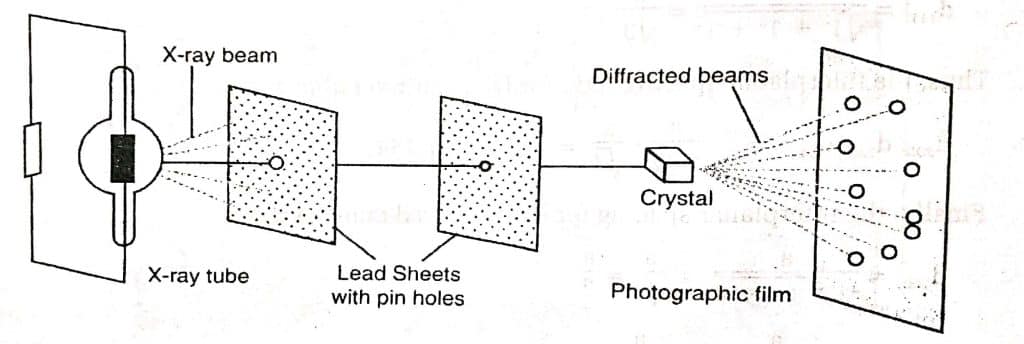
Since a crystal solid is made up of many parallel and equidistant atomic planes, Bragg considered that the X-ray diffraction effect might be explained as the X-ray being reflected by successive planes of atoms in the crystal. As a result, when X-rays strike a crystal face, they penetrate because the interplanar distance between most of the crystal and the wavelength of the X-ray is comparable, and X-rays have greater penetrating power than low-energy electrons.
.
Derivation of Bragg’s equation
let us consider BB1, CC1 and DD1 are a set of parallel and equidistance planes of a crystal and the inter-planer distance between these planes are equal to ‘d’. Let’s consider a beam of monochromatic X-rays PQ is incident on plane BB1 with angle θ and reflected along QR. Similarly, another beam XY is incident on the second plane CC1 with angle θ and reflected among YZ.
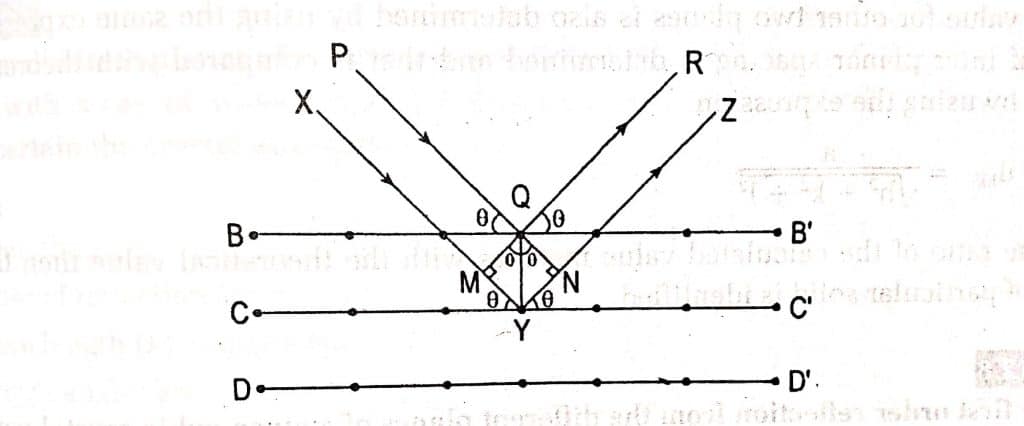
The path difference between the reflected ray is equal to MY +NY and MY=NY=dsinθ
path difference = MY +NY
= d sinθ + d sinθ
= 2d sinθ, Where d = interplanar distance
Now, in order for reflected rays to be in phase (for constructive interference), the path difference between them must be an integral multiple of the X-ray wavelength (λ), i.e.
nλ = 2d sinθ
This equation is called Bragg’s equation.
Where n=1,2,3,…..specifies the order of reflection.
[For first-order reflection n=1 and n=2 for second-order reflection and so on].
Application of Bragg’s equation
Bragg’s equation is applicable for the determination of the inter-planar distance of the crystal lattice.
Bragg’s equation Video
FAQs/MCQs
What is the bragg equation?
Bragg’s equation is a mathematical equation, derived by W. L. Bragg and W. H. Bragg, describes the relation between interatomic distances from X-ray diffraction patterns.
bragg’s law equation
Bragg’s law equation is 2d sinθ = nλ, where d is interplanar distance, n= order of reflection, λ = wavelength.
References
- Bragg, W.L. The Crystalline State: Volume I. New York: The Macmillan Company, 1934.
- Arun Bahl, B. S. Bahl & G. D. Tuli, Essentials of Physical Chemistry, S. Chand and Company Ltd., New Delhi, 2012.