Beer’s law is an empirical law that relates the concentration of colored substances and the absorption of light. Beer’s law is applicable for dilute solutions and deviations are observed for concentrated solutions. There is no exception of Lambert’s law. This law was given by Beer in 1852
Beer’s law definition
According to Beer’s law, “When a beam of monochromatic light is passed through a solution of a homogeneous absorbing medium, the rate of decrease in intensity of light with respect to the concentration of the solution is directly proportional to the intensity of light.“
Beer’s law derivation
Mathematically, Beer’s law can be represented as:
–dI/dC ∝ I
–dI/dC = K’I ……………………………………………….(i)
where –dI/dC= rate of decrease of intensity of light with respect to the concentration of the solution.
K’= a proportionality constant whose value depends on the nature of the absorbing medium and wavelength used.
I=Intensitiy of light at any concentration.
On rearrangement of equation (i), we get
-dI/I=K’dC
If Io is the intensity of incident radiation when C=0, then the intensity of radiation It after passing through the solution having concentration C can be obtained by integrating the above equation.
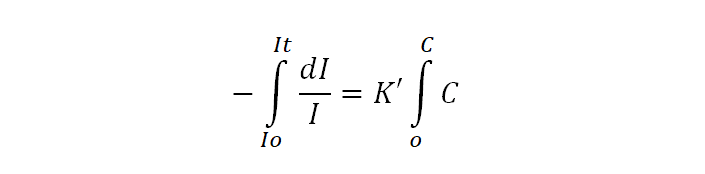
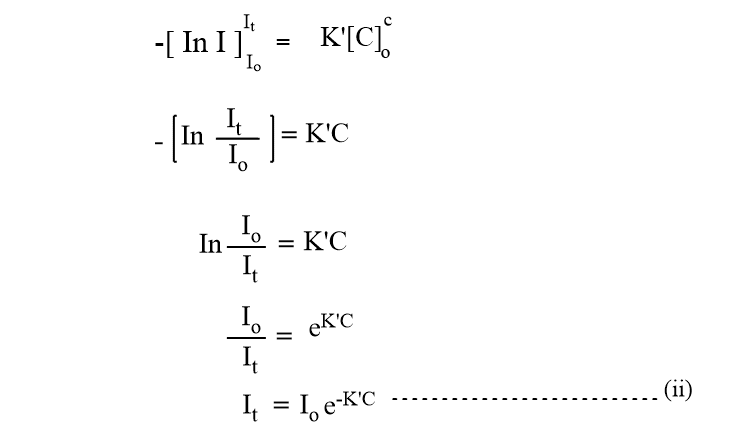
From this equation, it is clear that the intensity of a monochromatic beam of light decreases exponentially as the concentration of absorbing substance increases. Changing natural logarithm to the base 10, equation (ii) becomes,
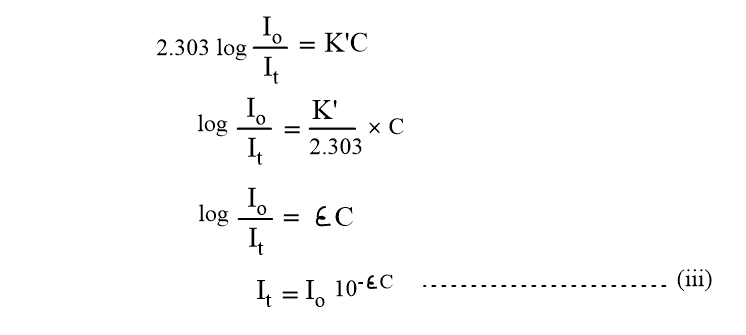
Where, ε = K’/2.303, is known as the extinction coefficient, and its unit is dm3 mol-1. Equations (ii) and (iii) are the mathematical expression of Beer’s law.
For the graphical representation of Beer’s law, the plot of ln(Io/It) vs C is drawn, and a straight line is obtained having a slope equal to K’.